1 Introduction
Selfishness refers to that an individual is self-interest, regardless of the interest of others. Fairness concern means that an individual is averse to disadvantageous or advantageous inequality between him and his partner. Altruism concern means that an individual cares about not only his own monetary payoff but also the monetary payoff of others. The neoclassical economic theory believes that the individual is selfish, i.e., the objective of a firm is seeking for the maximum profit. However, in April 2000, Starbucks signed a historic contract with TransFair USA, the purchases of Fairtrade certified coffee achieved 39 millions pounds in 2009, doubled the purchases in 2008
[1]. In 2008, earthquake in Wenchuan, China, many firms, such as China Vanke Co., Ltd. and the JDB group donate a lot of money and materials to help the affected people
[2]. In the experimental economics, we can also observe many non-selfish behaviors, for example, the pure altruistic behavior of proposers in the dictator game
[3, 4], the reciprocity, fair behavior in the public goods game, ultimatum game and trust game
[5-7]. Thus, there is an interesting question, some firms use selfish strategy and some firms use non-selfish strategy. Why? How these preferences affect the wholesale price strategy of the manufacturer and the retail price strategy of the retailer in a supply chain?
The non-selfish behaviors cannot be explained by the traditional economic theory because it deviates from the assumptions — An individual is selfishness in the neoclassical economic theory. This paper tries to explain the non-selfish behaviors by employing evolutionary game theory, and analyzes the effect of preferences on the price strategies of manufacturers and retailers. In the economic system, there are many homogenous supply chains, each supply chain consists of one manufacturer and one retailer, the non-selfish behavior of each manufacturer and retailer is fairness concern or altruism concern, we discuss the equilibrium outcomes in the short-term and the evolutionary dynamics in the long-term. We find the fair strategy and altruistic strategy may be the evolutionary stable strategy, the stability of the strategy depends on the parameters of preferences. The results to a certain extent explain the reasons that there are some non-selfish behaviors in the firm's decision and provide some suggestions to the managers.
2 Literature Review
The paper is related to the evolution of individual preference and the dynamics of supply chains.
Study on the individual preference has attracted many researchers in recent years. Fehr and Schmidt
[8], Bolton and Ockenfels
[9], Charness and Haruvy
[10] discussed the effect of fairness, altruism, reciprocity, cooperation and competition on the equilibrium outcome in the one-shot game using simple mathematical models. In fact, the short-term equilibrium state is broken usually in the real life, the evolutionary dynamics of individual preference is also an important topic that scholars interested in. Bester and G
th
[11], Dekel, et al.
[12], Bolle
[13], Ely and Yilankaya
[14], Ok and Vega-Redondo
[15], Sethi and Somanathan
[16], Sandholm
[17], Chai
[18] and Shirata
[19] analyzed the evolutionary dynamics of individual preference, including fairness, altruism, reciprocity, etc. However, the few papers investigate the evolutionary dynamics of individual preference in supply chains.
The dynamics of supply chains have been extensively studied. Xiao and Chen
[20], Xiao and Yu
[21, 22] studied the evolutionary stability of profit maximization and revenue maximization in supply chains. Yi and Yang
[23] analyzed the evolutionary stable strategy of retailers under network externality. Cui, et al.
[24] investigated the effect of inequality aversion on the behaviors of supply chain, and find that the inequality aversion can coordinate the supply chain under some conditions. Katok and Pavlov
[25], Ho, et al.
[26] analyzed the effect of fairness on supply chain contracts. Amaeshi, et al.
[27], Panda
[28], Goering
[29], Hua and Li
[30], Hsueh
[31], Ni, et al.
[32], Lau and Lau
[33] considered the effect of social responsibility preference on the supply chains, and got the conditions that social responsibility preference coordinates the supply chain. Chai
[18] studied the evolutionary dynamics of fairness in the supply chain under the assumption that the market demand is nonlinear. There are many researchers study the effect of the other preference on the supply chain
[34-37]. But there are few papers consider the effect of altruistic behavior on the dynamics of the supply chain.
The difference between our paper and the existing literature as follows: First of all, the existing literature about the preference in supply chains focuses on the effect of preference on coordination in supply chains, and consider the conditions that the preference coordinates supply chains in the short-term interaction. However, the equilibrium state in supply chains is always broken because of various factors, such as environment, the corporate structure. We consider the evolutionary dynamics of a supply chain once the equilibrium state is disturbed, and analyze the evolutionary stable strategies of manufacturers and retailers. Secondly, we consider the dynamics of supply chain in the short-term and long-term interaction when an individual has fair and altruistic preferences, simultaneously.
3 Models with Two Kinds of Preferences
There are many manufacturers and retailers in the economic system. Manufacturers and retailers match each other randomly to form a supply chain consisting of one manufacturer and one retailer. Manufacturers produce the final products and retailers sell the final products to consumers. A manufacturer and a retailer interact with each other to play a game. The time sequence of the game is as follows:
(ⅰ) The manufacturer announces his wholesale price () based on his management strategy;
(ⅱ) The retailer decides the retail price () based on his management strategy and the wholesale price.
In this paper, we analyze firstly the equilibrium state in the one-shot game. Furthermore, we study the evolutionary dynamics of supply chains once the equilibrium state disturbed due to the impacts of the environment, the adaption of corporate structure, and so forth. Specifically, we try to find the dynamics of supply chains over time, i.e., whether the supply chain can return the equilibrium state once the equilibrium state in the short-term disturbed. In Subsections 3.1, 3.2 and 3.3, we consider the dynamics of supply chains when each firm (manufacturer or retailer) only has two kinds of preferences, then we extend the results to the case with three pure strategies.
3.1 Dynamics of Supply Chain with Fair and Selfish Behaviors
In this subsection, we analyze the effect of fairness concern on the supply chain. Fairness concern is a common preference. We analyze fairness concern based on inequality aversion, where the fairness concern player arises disutility due to unfair behavior. If a manufacturer or retailer is selfish, his goal is seeking for the maximum profit; if a manufacturer or retailer is fairness concern, his objective is to maximize the utility that consists of material payoff and disutility due to unfair behavior. We assume that the market demand is a linear function, , where is the market scale, i.e., the largest demand (); is the sensitivity coefficient of product price; and is the unit production cost of manufacturers.
When the manufacturer and the retailer owns inequality aversion, the goals of both firms are to maximize the combination of material payoff and the disutility due to inequality. Let
denote the retailer's utility. According to the above analysis, the retailer's utility is
. The last term
denotes the disutility due to inequality. The algebraic form is
, see
[8], where
are the fairness concern parameters of the retailer.
is the parameter due to the disadvantage inequality,
is the parameter due to the advantage inequality. Cui, et al.
[24] pointed out that although the mathematical form of fair behavior is simple, but "the formulation strikes a reasonable balance between modeling tractability and behavioral complexity". In this paper, superscript
denotes selfish,
denotes fairness concern; subscript
denotes the manufacturer and
denotes the retailer. Hence, the optimization problem of a fairness concern retailer is
If the manufacturer is fairness concern, his utility function is , where are the fair parameters of manufacturers, describing the degree of manufacturers care about fairness. is the fair parameter due to advantage inequality, and is the fair parameter due to disadvantage inequality. The optimal problem of a fairness concern manufacturer is
According to Camerer and Fehr
[38], Levitt and List
[39], the fair parameter is not very high. We mainly discuss the dynamics of the game with
and
. For the other range of fairness concern, we can get the results using the similar analysis methods. The equilibrium outcomes in the one-shot game as
Table 1.
Table 1 The equilibrium outcome in the one-shot game |
The first column in Table 1 denotes the strategy profile of the manufacturer and retailer. The proof of Table 1 will be shown in Appendix A.
From Appendix A, when
, fairness concern of the manufacturer or retailer induces the lower wholesale price and retail price, and the impact on the retail price even more.
Figure 1 shows this situation, where the values of parameters are
in
Figure 1(a),
in
Figure 1(b). Furthermore, fairness concern of the manufacturer or retailer increases the retailer's profit, decreases the manufacturer's profit, and reduces the difference between the profits of manufacturers and retailers. Similar to Cui, et al.
[24], we can obtain the other equilibrium decisions in the one-shot game. We mainly discuss the evolutionary dynamics of manufacturers and retailers in the long-term interaction.
Figure 1 Equilibrium prices vs. fairness parameters |
Full size|PPT slide
In the following, we study the evolutionary stable strategies of manufacturers and retailers. In the human and social development, researchers have found that more successful strategies are more likely to be accepted and imitated, that is, the strategy of getting more payoffs is more likely to be chosen in the evolutionary process. The model is polymorphic in the paper, i.e., manufacturers and retailers choose their strategies in two or more than two pure strategies. Hence, we can assume that the evolution of the supply chain satisfies the replicator dynamics. Under the replicator dynamics, the growth ratio of a strategy closes to the advantage of this strategy. Specifically, the growth ratio of a strategy equals to the difference between the expected material payoff of the strategy and average material payoff in this population. Let the fraction of selfish manufacturers in the population be , the fraction of selfish retailers in the population be . We get the replicator dynamics of manufacturers and retailers as follows:
where denotes the expected material payoff of selfish manufacturers; denotes the expected material payoff of fair manufacturers; denotes the expected material payoff of retailers who use selfish strategy; and denotes the expected material payoff of retailers who use fair strategy. According to the eigenvalues of the Jacobian matrix of Equation (3) at the equilibrium points, we get the Proposition 1 as follows.
Proposition 1 When , equilibrium point is asymptotically stable; when , the equilibrium point is asymptotically stable.
The proof will be shown in Appendix B.
From Proposition 1, when retailers is moderate averse inequality, if the degree of manufacturers averse inequality is less than that of retailers, then manufacturers should use selfish strategy and retailers adopt fair strategy. That means that manufacturers using selfish strategy and retailers using fair strategy will get higher average profits than the other strategy profiles in the long-term interaction. If manufacturers to a certain extent care about fairness (), then the strategy profile where manufacturers and retailers use fair strategy is evolutionary stable, in this case, manufacturers' and retailers' profits are higher than the average profit in the long-term interaction. Further, we find that when the degrees of fairness concern of manufacturers and retailers are relatively high, it is advantage for both firms using fair strategy; if there is a firm cares about fairness not so much as another, the firm with higher fairness concern should use fair strategy and that firm with less fairness concern should use selfish strategy in the long-term game.
According to the expression of equilibrium profits of manufacturers and retailers, the dynamics of the game is independent of the market scale , sensitivity coefficient of product price and the unit production cost of manufacturers . So in the numerical examples, we fix the values of the parameters as . When the fairness parameter of manufacturers is relatively low, Figure 2 shows the dynamics of the supply chain, where the values of parameters are ; Figure 3 shows the dynamics of the supply chain when the fairness parameter of manufacturers is relatively high, and the values of parameters are .
Figure 2 Dynamics of game when manufacturers care about fairness at a relatively low level |
Full size|PPT slide
Figure 3 Dynamics of game when the degree of manufacturers' fairness is relatively high |
Full size|PPT slide
From Figures 2 and 3, we find that the dynamics of the game under different conditions are distinct. Figure 2 implies that the retailers will return to use fair strategy quickly even the equilibrium state in short-term game broken, whereas the manufacturers return to the equilibrium state that use selfish strategy slowly. Under the conditions in Figure 3, the retailers and the manufacturers return to the equilibrium state that both firms use fair strategy quickly for getting higher profits after the equilibrium state in short-term broken.
3.2 Dynamics of Supply Chain with Altruistic and Selfish Behaviors
In this subsection, we discuss the dynamics of the supply chain when pure management strategies are: Selfishness and altruism. Altruistic behavior is different from fair behavior, fairness concern means players arise disutility due to inequality aversion, while altruistic behavior refers to a certain extent the interest of others is included in the objective function of the player. We use superscript
denotes the altruistic behavior of players. According to Bester and G
th
[11], the optimization problems of altruistic manufacturers and retailers are
respectively. Here, is the altruistic parameter of manufacturers, i.e., the degree of altruism of manufacturers; is the altruistic parameter of retailers, describing the degree of altruism of retailers. The altruistic parameter or implies that the manufacturers or retailers are selfish. By directly calculating, we get the equilibrium prices
respectively.
The equilibrium profits of manufacturers and retailers are
respectively.
Similarly, we can obtain the equilibrium outcomes under the other strategy profiles. The equilibrium expression is shown in Table 2.
Table 2 The equilibrium outcome in the one-shot game with selfishness and altruism |
| | Equilibrium price | Equilibrium profit |
| | |
| | |
| | | |
| | |
| | |
According to the expression of the retailer's profit, we assume to ensure the nonnegative profit for retailers.
Figure 4 shows the effects of altruistic behavior of manufacturers and retailers on the wholesale price and retail price. Figure 4 (a) shows that the equilibrium prices of manufacturers and retailers increase with the growth of the degree of altruism for retailers; Figure 4 (b) shows that the equilibrium wholesale price and retail price decrease with the growth of degree of altruism for manufacturers. Here the values of parameters are in Figure 4 (a) and in Figure 4 (b).
Figure 4 Equilibrium prices vs. altruism parameters |
Full size|PPT slide
From Figure 5, we know that the altruistic behavior of manufacturers and retailers can increase the profit of their opponent, whereas the behavior will hurt their own profits. Figure 5 (a) shows that the altruistic behavior of the retailer makes the difference between his profit and the profit of the manufacturer bigger and bigger. Combing Figures 5 (a) and 4 (a), the reason should be the growth rate of wholesale price always is higher than the growth rate of retail price when the retailer is altruism. Figure 5 (b) shows that the profit of the manufacturer is decreasing with his altruism, and the profit of the retailer is increasing with the manufacturer's altruism. Furthermore, the profit of the manufacturer is less than the profit of the retailer once the degree of altruism of the manufacturer is high enough. Combing Figures 4 (b) and 5 (b), we find that this phenomenon arises because that the manufacturer's altruistic strategy makes the speed of decline of wholesale price always higher than that one of retail price. Here the values of parameters are in Figure 5 (a) and in Figure 5 (b).
Figure 5 Equilibrium profits vs. altruism parameters |
Full size|PPT slide
For further considering the evolutionary stable strategies of manufacturers and retailers when manufacturers and retailers are altruism or not, we analyze the dynamics of the supply chain using the replicator equations. Let denote the fraction of selfish manufacturers in the population, and denote the fraction of selfish retailers in the population. Similar to Subsection 3.1, we get the replicator equations of manufacturers and retailers as follows.
Here, the first term in parentheses of both equations in System (6) is the expected material payoff of the selfish manufacturer and retailer, respectively; the second term is the expected material payoff of the altruistic manufacturer and retailer, respectively. Based on the stability theory of differential equation, we get the result as Proposition 2.
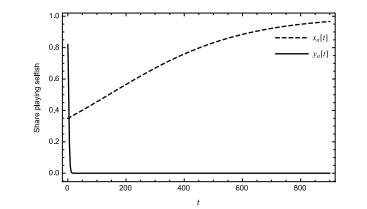
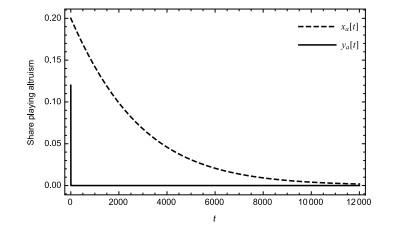
Proposition 2 Equilibrium point is asymptotically stable, i.e., both manufacturer and retailer choose selfish strategy is an evolutionary stable strategy; the other equilibrium points , and are unstable.
The proof refers to the proof of Proposition 1. For explaining the results better, we draw the dynamics figure of the game as Figure 6 and the advantage profit figure as Figure 7 using the numerical example. Here, the values of parameters are . and denote the advantage profits of selfish manufacturer and retailer, respectively.
Figure 6 Dynamics of game with selfishness and altruism |
Full size|PPT slide
Figure 7 The advantage profits of selfish strategy for manufacturers and retailers |
Full size|PPT slide
Combing Proposition 2 and Figure 6, the strategy where manufacturers and retailers decide their wholesale price and retail price basing on profit maximization is evolutionary stable. Furthermore, we find that when manufacturers and retailers choose one of two strategies: selfishness and altruism, the selfish strategy is the better strategy and the evolutionary stable strategy in the long-term interaction. According to Figure 7, the expected material payoff of a selfish manufacturer is always higher than the expected profit of the manufacturer using other strategy. So the selfish strategy is the dominant strategy for a manufacturer. Similar to the manufacturers, the retailers should also use selfish strategy in the long-term interaction.
3.3 Dynamics of Supply Chain with Fairness Concern and Altruism
Based on Subsections 3.1 and 3.2, we consider that two pure strategies of manufacturers and retailers are non-selfish. Firstly, we assume that manufacturers care about fairness, retailers care about altruism. Fair utility function is different with altruistic utility function. Fair utility is the combination of the players' material payoff and the disutility due to inequality; Bester and G
th
[11] point out that the altruistic utility is related to the behavior of both players, if the retailer is altruist, his utility is related to his profit and the profit of the manufacturer. According to Subsections 3.1 and 3.2, the objective functions of fairness concern manufacturer and altruistic retailer are respectively
In the case that manufacturers are altruist and retailers care about fairness, the optimization problems of altruistic manufacturer and fairness concern retailer are respectively
We can get the equilibrium outcome in the one-shot game by directly calculating, the results as Table 3 shows.
Table 3 The equilibrium outcome in the one-shot game with altruism and fairness |
Table 3 lists the equilibrium profits in the one-shot game under given strategy and conditions. We analyze the effects of altruism parameter and fairness parameter on the wholesale price and retail price in Subsections 3.1 and 3.2, where one of the two pure strategies is selfish strategy. Now we discuss the relationship between the preference parameters and equilibrium outcomes when two pure strategies are non-selfish. We mainly study the dynamics under the first case in Table 3, the relationship between the preference parameters and equilibrium prices as Figure 8 shows. The parameter value is in Figure 8 (a), in Figure 8 (b). From Figure 8, the fair preference of retailers induces manufactures and retailers to decrease their wholesale price and retail price. However, the altruism preference of retailers induces manufacturers to increase their wholesale prices. Comparing with the results in Subsections 3.1 and 3.2, the trends of equilibrium price changes are similar, but the speeds of change are different.
Figure 8 Equilibrium prices vs. fairness and altruism parameters of retailers |
Full size|PPT slide
Combining Figure 8 and the results in Subsections 3.1 and 3.2, we find that even the strategy spaces of manufacturers and retailers are different, the effects of a non-selfish preference on the equilibrium outcomes are similar. For getting the effect of strategy space on the dynamics of the game, and the stability of the equilibrium state broken when all strategies of manufacturers and retailers are non-selfish, we discuss the evolutionary stable strategies of manufacturers and retailers using the replicator dynamics. Let the fraction of altruistic manufacturers be in the population, the fraction of altruistic retailers be in the population. We get the replicator dynamics of manufacturers and retailers as follows.
The first term in the brackets of Equation (11) denotes the expected profits of altruistic manufacturers and retailers, respectively; the second term denotes the expected profits of manufacturers and retailers who use fair strategy. Hence, we have Proposition 3 by the stability theory of differential equation.
Proposition 3 When the manufacturers and retailers choose their management strategy in fair strategy and altruistic strategy, the results in the following are true.
When and , if , then the equilibrium point is asymptotically stable; if , then the equilibrium point is asymptotically stable;
When and , equilibrium point is asymptotically stable, the other equilibrium points are unstable;
When , if , then equilibrium point is stable but not asymptotically stable.
The proof refers to the proof of Proposition 1.
From Case 1) in Proposition 3, when the degree of fairness concern for retailer is relatively high (higher than 1/3 but less than 1/2), both the degree of fairness concern and altruism for manufacturer are less than the degree of fairness concern for retailer, and the degree of fairness concern for manufacturer is less than the degree of his altruism, then manufacturers and retailers should use fair strategy; if the degree of fairness concern for a manufacturer comparing with his altruism is relatively high, then the manufacturer should use altruistic strategy, the retailer should use fair strategy in the long-term interaction for getting higher profit. When the degree of fairness concern for retailers is relatively low (lower than 1/4), and the degree of non-selfish preference of manufacturers is higher than the degree of retailers' fairness concern, if the degree of manufacturers' fairness concern is less than that one of his altruism, both manufacturer and retailer should use fair strategy; if the degree of manufacturers' fairness concern is relatively high, then the strategy profile where they use altruistic strategy and retailers use fair strategy is evolutionary stable.
The dynamics of the game under Case 1) in Proposition 3 will be shown in Figures 9 and 10, where the values of parameters are in Figure 9, in Figure 10.
Figure 9 Dynamics when the degree of fairness for manufacturers is less than the degree of altruism |
Full size|PPT slide
Figure 10 Dynamics when the degree of fairness for manufacturers is higher than the degree of altruism |
Full size|PPT slide
From Case 2) in Proposition 3, when the degree of retailers' fairness is relatively high (higher than 1/4 and less than 1/2), the degree of manufacturers' fairness is less than that one of retailers, and the degree of manufacturers' altruism is higher than the degree of their fairness concern, then the strategy profile where manufacturers use altruistic strategy and retailers use fair strategy is evolutionary stable; when the degree of retailers' fairness is relatively low (lower than one forth), the degree of manufacturers' altruism is not high but higher than the degree of retailers' fairness, then the manufacturers should use altruistic strategy and the retailers should use fair strategy to decide their wholesale price and retail price for higher profits. The dynamics of the game under this case will be shown in Figure 11, where the values of parameters are .
Figure 11 Dynamics of game when the degree of altruism for manufacturers is relatively high |
Full size|PPT slide
Manufacturers and retailers are non-selfish, the evolutionary dynamics of the game is different in the long-term interaction, even the equilibrium outcomes in the one-shot game are similar. When the two pure strategies of manufacturers and retailers are selfish and altruistic, selfish strategy for both manufacturer and retailer is an evolutionary stable strategy. When two pure strategies of manufacturers and retailers are altruistic and fairness concern, although the strategy profile in which both manufacturer and retailer use altruistic strategy is unstable, but the strategy profile in which one player uses altruistic strategy and the other player uses fair strategy is evolutionary stable under some conditions, the manufacturer and the retailer can get higher profits in the long-term interaction in this case.
4 Dynamics of Supply Chain with Altruism, Fairness Concern and Selfishness
Section 3 discusses the case that the pure strategy sets of manufacturers and retailers include two strategies. Furthermore, we analyze the evolutionary stable strategies of manufacturers and retailers using the replicator dynamics.
In this section, we investigate the evolutionary dynamics of the supply chain when manufacturers and retailers choose their strategy in three pure strategies: Altruism, fairness concern, and selfishness. We denote the three strategies as strategy 1, strategy 2 and strategy 3, respectively. Let the probability of a manufacturer using strategy be ; the probability of a retailer choosing strategy be . Then the strategy spaces of a manufacturer and retailer are and , respectively.
Based on Tables 1–3 in Section 3, we get the payoff matrix when and . Let denote the fraction of altruistic manufacturers and retailers, respectively; denote the fractions of manufacturers and retailers who care about fairness, respectively; denote the fractions of selfish manufacturers and retailers, respectively. Here . Similarly, we get the replicator dynamics of manufacturers and retailers in the game as follows:
where denotes the expected payoff of the manufacturer who uses strategy , is the average payoff of all manufacturers in the population; is the expected payoff of the retailer using strategy , and is the average payoff of all retailers in the population.
Similar to Proposition 1, we derive Proposition 4.
Proposition 4 The evolutionary stable strategies of manufacturers and retailers in the following:
When , the equilibrium point , , i.e., the strategy profile in which manufacturers use selfish strategy and retailers use fair strategy is asymptotically stable, the other equilibrium points are unstable;
When and , there is no any asymptotically stable equilibrium;
When , the equilibrium point , is asymptotically stable.
From Proposition 4, when manufacturers care about fairness relatively low and retailers care about fairness concern moderately, then the manufacturers decide their wholesale prices using selfish strategy and the retailers give their retail price using fair strategy, that is, the manufacturers and the retailers get higher profits than other strategy profiles in the long-term interaction. When manufacturers care about fairness moderately and altruism relatively high, then the strategy profile in which manufacturers use altruistic strategy and retailers use fair strategy is evolutionary stable. Comparing with the results in Section 3, we get the strategy space can affect the evolutionary dynamics. Furthermore, we find that the evolutionary stable strategy in a supply chain depends on the degrees of manufacturers' and retailers' preferences; fair strategy is better than selfish and altruistic strategies; and firms using fair strategy will get competitive advantage.
5 Conclusions
In this paper, we analyze the evolutionary stable strategies in supply chains. Manufacturers and retailers match each other randomly. Firstly, we discuss the evolutionary stable strategies of manufacturers and retailers when they choose their management strategies from two pure strategies. Then we study the evolutionary stable strategy in the three strategy setting.
When the two pure strategies are fair strategy and selfish strategies, we find that if inequality aversion of retailers is not very high, and the inequality aversion of manufacturers is less than that of manufactures, then the strategy profile in which manufactures use profit maximization and retailers use utility maximization is evolutionary stable; when manufacturers are averse to inequality to a certain extent, utility maximization for both firms is evolutionary stable.
When two pure strategies are selfish strategy and altruistic strategy, the symmetry selfish strategy is an evolutionary stable strategy. When two pure strategies are altruistic strategy and fair strategy, the evolutionary dynamics depends on the degrees of preference for manufacturers and retailers. For manufacturers, fair strategy and altruistic strategy may be chosen under different conditions. However, for retailers, fair strategy is a profitable strategy in spite of what is the strategy of manufacturers. The reason is that the fair preference of a retailer decreases both wholesale price and retail price, while the altruism preference of a retailer increases the wholesale price while decreases the retail price, thus the profit of the retailer always decreases when the retailer is an altruist.
When the pure strategies of manufacturers and retailers are selfishness, altruism or fairness concern, the dynamics of the supply chain is different from the dynamics under two kinds of preferences. Thus, we find the strategy spaces of manufacturers and retailers can also affect the evolutionary strategy.
Research on the effect of individual preference on the strategy is an interesting topic, we consider the evolutionary dynamics of supply chains with three individual preferences, we find the evolutionary stable strategy of manufacturers and retailers is close to the degree of individual preferences. However, there are still have several aspects that can be studied in the future. Firstly, in our models, we assume that the match between the manufacturer and retailer is random, the non-random match is also a common situation in the real life. Secondly, the demand and cost are certain in our models, the study on the effect of uncertain factors on the evolutionary dynamics is also one of our further researches. Finally, we only consider the evolution of management strategy of firms, the evolution of non-selfish preferences of firms will be discussed in the future.
Appendix A
The proof of Table 1.
1) The profit of manufacturers is higher than that of retailers
Based on Cui, et al.
[24], the objective function of a retailer who cares about fairness is
The second-order derivative of the objective function with respect to is , i.e., is a concave function of . Solving the first-order condition for under conditional on retailers' disadvantageous inequality, we get the response function of retailers: . Thus, conditional on disadvantageous inequality, we get the optimal price for retailers as follows:
where, according to the condition that the retailers' profits are lower than the manufacturers' profits: . Solving , we get .
The objective function of a manufacturer who cares about fairness concern is
The second-order derivative of with respect to is
i.e., is a concave function of . By indirect calculating, we get that when , the equilibrium wholesale price of manufacturer is
When , the equilibrium profits of manufacturer and retailer are
respectively. If else .
The objective function of a selfish manufacturer is , s.t. . Similarly, the equilibrium prices of manufacturer and retailer are , respectively. The equilibrium profits of manufacture and retailer are , respectively.
2) The profit of retailers is higher than that of manufacturers. The objective function of a retailer who cares about fairness is , s.t. . The second-order derivative of the objective function with respect to is , i.e., is a concave function of . Solving the first-order condition for under conditional on retailers' advantageous inequality, we obtain the response function of retailers . Thus, the optimal price for retailers is
where . The optimal problem of a fairness concern manufacturer is , s.t. . There is no feasible solution in the feasible region, so the profit of manufacturer is always higher than that of the retailer.
Appendix B
The proof of Proposition 1. We only prove Case 1) of Proposition 1.
According to the replicator dynamics (3), we get the Jacobian matrix
Substituting into Jacobian matrix, we get that the Jacobian matrix at equilibrium point (1, 0) is Hence the two eigenvalues of Jacobian matrix at (1, 0) are
, respectively. According to the stability theory of differential equation, we get that the equilibrium point (1, 0) is local asymptotically stable. Similarly, we can prove Case 2) in Proposition 1. Hence the Proposition 1 is true.
Appendix C
The proof of Table 3.
According to Appendix A, we find that the profit of the retailer is always less than the profit of the manufacturer. So we only consider the case that the profit of manufacturer is higher than the profit of the retailer in Appendix C.
1) When manufacturers care about altruism and retailers care about fairness. The objective of a retailer is , s.t. . From the first-order condition, we get the optimal price of the retailer as follows: when ; if else . So the objective of an altruistic manufacturer is , s.t. . By the second-order derivative of the objective function with respective to , , we know the objective function is a concave function of . Then when , the equilibrium prices of the manufacturer and the retailer are
respectively; if else . Furthermore, when , we get that the equilibrium profits of manufacturers and retailers are
respectively. If else .
2) Manufacturers care about fairness and retailers are altruist
The objective function of the retailer is . The second-order derivative of the objective function with respect to is , so the objective is a concave function of . Hence, according to the first-order condition, we get that the response function of retailer is . Furthermore, we get that the optimal problem of manufacturers is , s.t. . The second-order derivative of the objective function with respect to is . So the objective function is a concave function of . The equilibrium prices of manufacturers and retailers are
respectively.
Combing the results in Subsections 3.1–3.3, we get the results in Table 3. So Table 3 is true.
{{custom_sec.title}}
{{custom_sec.title}}
{{custom_sec.content}}
 PDF(319 KB)
PDF(319 KB)


 PDF(319 KB)
PDF(319 KB)
 PDF(319 KB)
PDF(319 KB)
 PDF(319 KB)
PDF(319 KB)
 Table 1 The equilibrium outcome in the one-shot game
Table 1 The equilibrium outcome in the one-shot game Figure 1 Equilibrium prices vs. fairness parameters
Figure 1 Equilibrium prices vs. fairness parameters Figure 2 Dynamics of game when manufacturers care about fairness at a relatively low level
Figure 2 Dynamics of game when manufacturers care about fairness at a relatively low level Figure 3 Dynamics of game when the degree of manufacturers' fairness is relatively high
Figure 3 Dynamics of game when the degree of manufacturers' fairness is relatively high Table 2 The equilibrium outcome in the one-shot game with selfishness and altruism
Table 2 The equilibrium outcome in the one-shot game with selfishness and altruism Figure 4 Equilibrium prices vs. altruism parameters
Figure 4 Equilibrium prices vs. altruism parameters Figure 5 Equilibrium profits vs. altruism parameters
Figure 5 Equilibrium profits vs. altruism parameters Figure 6 Dynamics of game with selfishness and altruism
Figure 6 Dynamics of game with selfishness and altruism Figure 7 The advantage profits of selfish strategy for manufacturers and retailers
Figure 7 The advantage profits of selfish strategy for manufacturers and retailers Table 3 The equilibrium outcome in the one-shot game with altruism and fairness
Table 3 The equilibrium outcome in the one-shot game with altruism and fairness Figure 8 Equilibrium prices vs. fairness and altruism parameters of retailers
Figure 8 Equilibrium prices vs. fairness and altruism parameters of retailers Figure 9 Dynamics when the degree of fairness for manufacturers is less than the degree of altruism
Figure 9 Dynamics when the degree of fairness for manufacturers is less than the degree of altruism Figure 10 Dynamics when the degree of fairness for manufacturers is higher than the degree of altruism
Figure 10 Dynamics when the degree of fairness for manufacturers is higher than the degree of altruism Figure 11 Dynamics of game when the degree of altruism for manufacturers is relatively high
Figure 11 Dynamics of game when the degree of altruism for manufacturers is relatively high