PMCMC for Term Structure of Interest Rates under Markov Regime Switching and Jumps

Xiangdong LIU; Xianglong LI; Shaozhi ZHENG; Hangyong QIAN

doi:10.21078/JSSI-2020-159-11

PDF(826 KB)

Journal of Systems Science and Information ›› 2020, Vol. 8 ›› Issue (2) : 159-169. DOI: 10.21078/JSSI-2020-159-11

PMCMC for Term Structure of Interest Rates under Markov Regime Switching and Jumps

Author information +

History +

Abstract

A parameter estimation method, called PMCMC in this paper, is proposed to estimate a continuous-time model of the term structure of interests under Markov regime switching and jumps. There is a closed form solution to term structure of interest rates under Markov regime. However, the model is extended to be a CKLS model with non-closed form solutions which is a typical nonlinear and non-Gaussian state-space model(SSM) in the case of adding jumps. Although the difficulty of parameter estimation greatly prevents from researching models, we prove that the nonlinear and non-Gaussian state-space model has better performances in studying volatility. The method proposed in this paper will be implemented in simulation and empirical study for SHIBOR. Empirical results illustrate that the PMCMC algorithm has powerful advantages in tackling the models.

Key words

PMCMC / term structure of interest rates / state-space models / regime switching / jumpdiffusion

Cite this article

EndNote

Ris (Procite)

Bibtex

Download Citations

Xiangdong LIU , Xianglong LI , Shaozhi ZHENG , Hangyong QIAN. PMCMC for Term Structure of Interest Rates under Markov Regime Switching and Jumps. Journal of Systems Science and Information, 2020, 8(2): 159-169 https://doi.org/10.21078/JSSI-2020-159-11

1 Introduction

The Kalman Filter (KF) has been widely applied many fields in linear state-space models with Gaussian noise such as engineer and economics. Even though nonlinear systems, the problem can also be tackled by the extended Kalman Filter (EKF) and unscented Kalman Filter (UKF). However, all these methods are only applicable to Gaussian models. Inspired by the proposal of sequential important sampling (SIS) by Hammersely, et al. in the 1950s, one can solve nonlinear and non-Gaussian problems through approximating the posterior distribution and likelihood method of the latent state variables in state-space models based on Bayesian rule and sequential Monte Carlo (SMC) scheme^[1-5]. However, the method suffered from a well-known particle degeneracy problem early and it has been improved efficiently through resampling method by Gordon, et al.^[6] so that its application is really achieved in various fields. Therefore, more resampling methods were proposed in subsequent researches such as stratified resampling^[7], residual resampling^[8] and systematic resampling^[9]. These methods are collectively called particle filter (PF)^[10-13]. The key to a better performance is to design a more efficient function. Pitt and Shephard^[14] proposed auxiliary particle filter in which the samples always based on the latest observation. More methods about particle filter can be found in [15–17].

A main application of particle filter is parameter estimation for nonlinear and non-Gaussian state-space models. This paper aims to implement an algorithm called PMCMC to estimate unknown parameters of a typical SSM model: The term structure of interest rates under Markov regime switching. PMCMC algorithm combines particle filter with the popular method MCMC, which is studied by several scholars. Johannes, et al^[18]. use particle filtering to extract latent stochastic variance from stochastic volatility models with and without jumps. Malik and Pitt^[19] adapted particle filtering within maximum likelihood method to study a basic stochastic volatility model with leverage effect. Carvalho and Lopes^[20] and Rios and Lopes^[21] used the particle filtering framework and its extension to estimate Markov switching stochastic volatility models. Christoffersen, et al.^[22] applied particle filtering to both estimate model parameters and filter latent variance factor for option pricing under several stochastic volatility models. In economics, some researchers also use particle filtering-based algorithm to estimate dynamic stochastic general equailibrium (DSGE) models, such as Fern

\overset{´}{a}

ndez-Villaverde and Rubio-Ram

\overset{´}{I}

rez^[23] and An and Schorfheide^[24]. These researchers use particle filtering to calculate likelihood function values for DSGE models, and then use either Bayesian method or numerical optimization to estimate parameters in the models^{[25, 26]}. Andrieu, et al.^[27] summarized this PMCMC idea as a general calculation framework and provide some theoretical foundations. The advantage of the method is that we can obtain the posterior distributions of both states and parameters. The term structure of interest rates is always the most important research object in finance. Models that incorporate regime-switching risk into interest rates can perform the stochastic behavior better than single regime^{[28, 29]}. Most of researches are achieved by models with closed form solutions. However, in more complex SSM models, the lack of a good estimation method makes it difficult, especially with jumps^[30]. This paper contributes to study the term structure of interest rates under regime switching and jumps with PMCMC algorithm. Empirical results illustrate that the PMCMC algorithm has powerful advantages in tackling the models. Also, new methods are proposed to prevent particles degenerating to enhance efficiency of the algorithm.

The rest of this paper is organized as follows. In Section 2, we proposed particle MCMC algorithm and further study the proposed procedure. In Section 3, simulation study is calculated. Empirical study and conclusion are given in Section 4 and Section 5 respectively.

2 Particle MCMC Algorithm

In this section, we aim at illustrating the process of PMCMC algorithm how to estimate parameters for multiple parameters of nonlinear and non-Gaussian state-space models. SSMs usually include two parts: One is an unobservable Markov state process

{X_{t}; t = 1 : T}

, the other is an observable measurement process

{Y_{t}; t = 1 : T}

. The model is given as follows

\begin{array}{rcl} Y_{t} = g (X_{t}) + u_{t}, \end{array}

(1)

\begin{array}{rcl} X_{t} = f (X_{t - 1}) + v_{t} . \end{array}

(2)

For nonlinear non-Gaussian state-space models, the terms

g (.)

and

f (.)

are not nonlinear with non-Gaussian

u_{t}

and

v_{t}

. Generally, the probability density functions

p (x_{t} | y_{t})

and

p (x_{t} | x_{t - 1})

are known, so the likelihood function can be given by

\begin{aligned} p_{θ} (y_{1 : T}) = \int p_{θ} (x_{1}) \prod_{n - 2}^{T} P_{θ} (x_{n} | x_{n - 1}) \prod_{n - 1}^{T} P_{θ} (y_{n} | x_{n}) d_{x_{1 : T}}, \end{aligned}

(3)

where

θ

is a known parameter vector. In this case, it is difficulty to calculate likelihood value through integrating directly. However, it is available through sequential Monte Carlo integration with Bayesian recursive. The process is shown as follows.

The conditional probability density function

P_{θ} (y_{t} | y_{1 : t - 1})

can be calculated by

\begin{array}{rcl} P_{θ} (y_{t} | y_{1 : t - 1}) & = & \int P_{θ} (y_{t} | x_{1 : t} | y_{1 : t - 1}) d_{x_{1 : t}} \end{array}

(4)

\begin{array}{rcl} = & \int w (x_{1 : t}) q (x_{1 : t} | y_{1 : t}) d_{x_{1 : t}} = E [w (x_{1 : t})], \end{array}

(5)

where

w (x_{1 : t})

is the unnormalized weight,

\begin{aligned} w (x_{1 : t}) = \frac{p_{θ} (y_{t}, x_{1 : t} | y_{1 : t})}{q (x_{1 : t} | y_{1 : t})}, \end{aligned}

(6)

we noted that

q (x_{1 : t} | y_{1 : t})

is an artificial importance density function which samples can be drawn from easily. It is usually given by the form

\begin{aligned} q (x_{1 : t} | y_{1 : t}) = q (x_{1 : t - 1} | y_{1 : t - 1}) \times q (x_{1 : t} | x_{1 : t - 1}, y_{1 : t}) . \end{aligned}

(7)

When

N

particles

{x_{1 : t}^{i}, i = 1 : N}

are generated from

q (x_{1 : t} | y_{1 : t})

in (7), the unbiased estimators

{\hat{p}}_{θ} (y_{t} | y_{1 : t - 1})

and

{\hat{p}}_{θ} (x_{1 : t}^{i} | y_{1 : t})

p_{θ} (y_{t} | y_{1 : t - 1})

and

p_{θ} (x_{1 : t}^{i} | y_{1 : t})

can be acquired by, respectively

\begin{array}{rcl} {\hat{p}}_{θ} (y_{t} | y_{1 : t - 1}) = \frac{1}{N} \sum_{i = 1}^{N} w (x_{1 : t}^{i}), \end{array}

(8)

\begin{array}{rcl} {\hat{p}}_{θ} (x_{1 : t}^{i} | y_{1 : t}) = \frac{w (x_{1 : t}^{i})}{\sum_{i = 1}^{N} w (x_{1 : t}^{i})} = W (x_{1 : t}^{i}) . \end{array}

(9)

Thus, the likelihood value can be calculated by

\begin{aligned} {\hat{p}}_{θ} (y_{1 : T}) = p_{θ} (y_{1}) \prod_{t = 2}^{T} {\hat{p}}_{θ} (y_{t} | y_{1 : t - 1}) . \end{aligned}

(10)

The key to an efficient particle filter method is to design a valid importance function. Resampling need to prevent variance of weights from increasing with time. The idea of resampling gives rise to

q (x_{1 : t - 1} | y_{1 : t - 1}) = p (x_{1 : t - 1} | y_{1 : t - 1})

in (7) executing next calculation, so one need to calculate resample

x_{1 : t}

every time through (9). Besides,

q (x_{t} | x_{1 : t - 1}, y_{1 : t})

is usually chosen as

p_{θ} (x_{t} | x_{t - 1})

for simplicity, while

p_{θ} (x_{t} | x_{t - 1}, y_{t})

in auxiliary particle filter performs more better. In former case, the weight

w (x_{1 : t})

calculated on the Markov of the state variables is equal to

p_{θ} (y_{t} | x_{t})

. If

\int p_{θ} (y_{t} | x_{t}) p_{θ} (x_{t} | x_{t - 1}) d_{x_{t}}

is convenient to integrate, we can set

q (x_{1 : t} | y_{1 : t}) = p (x_{1 : t - 1} | y_{1 : t - 1})

. That is the second term in (6) that is omitted. The approach is available in this paper. In this case, the weight is updated by

w (x_{1 : t}) = \int p_{θ} (y_{t} | x_{t}) p_{θ} (x_{t} | x_{t - 1}) {d x}_{t}

MCMC is a well-known sampler as Metropolis-Hasting (M-H) and Gibbs update. PMCMC implements MCMC in propagating new parameters for particle filter. Only M-H or Gibbs method is inadequate for multiple parameters, so a combination between MH and Gibbs is applied in this paper. The method with transition function

q (θ_{i} | θ_{i}^{k - 1})

and prior function

p (θ_{i})

is summarized in algorithm as follows:

Algorithm for

k

-th iteration in PMCMC where

θ^{k} = (θ_{1}^{k}, θ_{2}^{k}, \dots, θ_{n}^{k})

for

i = 1 : n

, sample from

p (θ_{i}^{k} | θ_{1}^{k}, \dots, θ_{i - 1}^{k}, θ_{i + 1}^{k - 1}, y_{1 : T})

as follows

1) Sample

θ_{i}^{k} \sim q (θ_{i} | θ_{i}^{k - 1})

;

2) Calculate

{\hat{p}}_{θ_{1}^{k}, \dots, θ_{i}^{k}, θ_{i + 1}^{k - 1}, \dots, θ_{n}^{k - 1}} (y_{1 : T})

by particle filter algorithm, adopt

θ_{i}^{k}

with probability

\begin{aligned} α = min (1, \frac{{\hat{p}}_{θ_{1}^{k}, \dots, θ_{i - 1}^{k}, θ_{i}^{k}, θ_{i + 1}^{k - 1}, \dots, θ_{n}^{k - 1}} (y_{1 : T}) p (θ_{i}^{k}) q (θ_{i}^{k - 1} | θ_{i}^{k})}{{\hat{p}}_{θ_{1}^{k}, \dots, θ_{i - 1}^{k}, θ_{i}^{k - 1}, θ_{i + 1}^{k - 1}, \dots, θ_{n}^{k - 1}} (y_{1 : T}) p (θ_{i}^{k - 1}) q (θ_{i}^{k} | θ_{i}^{k - 1})}), \end{aligned}

(11)

else

θ_{i}^{k} = θ_{i}^{k - 1}

3 Simulation Study

3.1 A Non-Linear State Space Model

Consider the non-linear state space model below, which used to be performed for Bayesian filter

\begin{array}{rcl} x_{t} = 0.5 x_{t - 1} + 25 \frac{x_{t - 1}}{1 + x_{t - 1}^{2}} + 8 \cos (1.2 t) + v_{t}, \end{array}

(12)

\begin{array}{rcl} y_{t} = \frac{x_{t}^{2}}{20} + w_{t}, \end{array}

(13)

where

v_{t} \sim i . i . d . N (0, σ_{v})

and

w_{t} \sim i . i . d . N (0, σ_{w})

. Let

σ_{v} = 3

and

σ_{w} = 3

, we can take 200 observations. We applied the MCMC, PMMH and PLMH algorithm in this model and the proposal with 1000 particles. The resampling scheme is multinomial resampling. We chose the last 20000 iterations for analysis. The results perform well in all algorithms. However, the auto-correlation function decreased to zero faster in PLMH than the other two algorithms.

3.2 The Regime-Switching Model

The regime-switching models incorporate nonlinearity into interest rate to capture the stochastic behavior. Generally, such models have a better empirical performance than single regime. A two-regime model of short-term interest rate based on CKLS is constructed in this section. It can be written as a differential equation

\begin{aligned} d_{r} = (α_{s_{t}} + k_{s_{t}} r) d_{t} + σ_{s_{t}} r^{γ_{s_{t}}} d W_{t} . \end{aligned}

(14)

The equation usually can be transferred to a discrete form

\begin{aligned} r_{t} = α_{s_{t}} + β_{s_{t}} r_{t - 1} + σ_{s_{t}} r_{t - 1}^{γ_{s_{t}}} ϵ_{t}, \end{aligned}

(15)

where

s_{t}

is the Markov state variable with two values 1 and 2. The term

α_{s_{t}} + β_{s_{t}} r_{t - 1}

is the drift function and

σ_{s_{t}} r_{t - 1}^{γ_{s_{t}}}

is the diffusion function. The noise term

ϵ_{t}

follows a standard normal distribution. We specify a parameter vector

θ

that contains all the parameters

α_{s_{t}}

β_{s_{t}}

σ_{s_{t}}

γ_{s_{t}}

and transition probability which can be expressed as follows.

\begin{array}{rcl} P (s_{t + 1} = 1 | s_{t} = 1) = p, P (s_{t + 1} = 2 | s_{t} = 1) = 1 - p, \end{array}

(16)

\begin{array}{rcl} P (s_{t + 1} = 2 | s_{t} = 2) = q, P (s_{t + 1} = 1 | s_{t} = 2) = 1 - q . \end{array}

(17)

So the parameter vector can be written as

θ = {(α_{1}, α_{2}, β_{1}, β_{2}, σ_{1}, σ_{2}, p, q)}^{'}

Figure 1 Trace plots, scatter plots and ACF of the parameters $σ_{v}$ and $σ_{w}$

Full size|PPT slide

3.3 The Results via PMCMC

We simulated sample size 200 observations according to the model discussed above with setting

α_{1} = 0.02

α_{2} = 0

β_{1} = 0.5

β_{2} = 1

σ_{1} = 0.05

σ_{2} = 0.02

γ_{1} = 0.5

γ_{2} = 0.5

and

p = 0.7

q = 0.7

. The initial state

s_{t}

is assumed to be equal to 1 and initial condition

r_{0} = 0.02

. We use particle filter for state estimation under the true parameters values. The estimate of Markov state variable

s_{t}

\begin{aligned} {\hat{s}}_{t}^{M M A P} = \arg max_{s_{t} = 1, 2} p (s_{t} | r_{1 : t}), \end{aligned}

(18)

the error rate is

\begin{aligned} e r r o r = 1 - \frac{1}{T} \sum_{t = 1}^{T} δ ({\hat{s}}_{t} - s_{t}), \end{aligned}

(19)

where

δ

is a Dirac-delta function. We compare APF

p_{θ} (x_{t} | x_{t} - 1, y_{t} - 1)

and the simplest possible proposal

p_{θ} (x_{t} | x_{t} - 1)

with different particle numbers. We ran the algorithm 100 times for each situation to calculate the mean and standard error.

Table 1 The comparison between APF and PF under N

N		500	1000	2000	5000	10000
APF	M-error	0.251	0.250	0.249	0.248	0.245
	M-loglik	714.881	714.895	714.890	714.885	714.896
	Sd-loglik	0.169	0.115	0.079	0.058	0.036
PF	M-error	0.252	0.249	0.249	0.246	0.246
	M-loglik	714.835	714.867	714.876	714.885	714.880
	Sd-loglik	0.407	0.266	0.181	0.111	0.081

Clearly the result improves as the particle number increases, especially the standard error. And the APF performed better than PF under the same particle number.

When the parameters is unknown, we set the prior

α_{1}, α_{2} \sim N (0, 0.05)

β_{1}, β_{2} \sim N (0.5, 0.5)

p, q \sim b e t a (4, 2)

and

σ_{1}, σ_{2} \sim i n v G a m m a (5, 5)

. The PMCMC algorithm was run for 30000 iterations with 2000 particles. In Figure 2, we display the trace plots and histograms of only parameters

α_{1}

and

α_{2}

. Both parameters show in trace plots move well in finite space and the histograms show posterior distributions of parameters. The estimation results are presented in Table 2 except

γ

for a comparison between true parameters and estimates. We can see that all estimators get closed to the true value with small standard deviation. The unit-root test suggests that Markov chains of all the parameters follow stationary processes. Hence, we can confirm the truth that the estimation results from PMCMC algorithm validly.

Figure 2 Trace plots and ACF of parameters for PF and APF

Full size|PPT slide

Table 2 Estimation via PMCMC

		α₁	α₂	β₁	β₂	σ₁	σ₂	p	q
	True	0.02	0	0.5	1	0.05	0.02	0.7	0.7
APF	Mean	0.0222	0.0024	0.487	0.926	0.044	0.0241	0.620	0.760
	SD	0.0070	0.0021	0.158	0.056	0.0045	0.0032	0.128	0.093
PF	Mean	0.0228	0.0027	0.476	0.921	0.0456	0.0255	0.599	0.779
	SD	0.008	0.0028	0.187	0.073	0.0054	0.0035	0.160	0.131

4 Empirical Study: Jump-diffusion Model with Regime

An empirical study is achieved in this section. The data used are from Shanghai Interbank Offered Rate (SHIBOR) with 7-days maturity from October 2006 to December 2014. There are 198 observations totally which are half-monthly average interest rates. The trace plot and summary statistics are presented below. We introduced Poisson jump as a new component into the model constructed above. The model can be expressed as

\begin{aligned} d r_{t} = (α_{s_{t}} + k_{s_{t}} r_{t - 1}) d t + σ_{s_{t}} r_{t - 1}^{γ_{s_{t}}} d W_{t} + J_{s_{t}} d N_{s_{t}}, \end{aligned}

(20)

where

J_{s_{t}}

represents jump size following a normal distribution

N (μ_{s_{t}}, η_{s_{t}})

and

N_{s_{t}}

is a Poisson process with intensity

λ_{s_{t}}

. We assume that there is at most one jump in a given time. The prior are set as

γ_{1}, γ_{2} \sim N (0, 0.5)

λ_{1}, λ_{2} \sim b e t a (2, 2)

μ_{1}, μ_{2} \sim N (0, 0.02)

η_{1}, η_{2} \sim i n v G a m m a (20, 10)

with the others the same as described above. When the number of parameters is large, we divided them into two parts:

θ_{1} = {(α_{1}, β_{1}, σ_{1}, γ_{1}, λ_{1}, μ_{1}, η_{1})}^{'}

and

θ_{2} = {(α_{2}, β_{2}, σ_{2}, γ_{2}, λ_{2}, μ_{2}, η_{2}, p, q)}^{'}

. We run PMCMC algorithm with a combination MH with Gibbs update for 30000 iterations and the last 20000 data are used. The particle number is 2000. The estimation results are displayed in Table 2. The trace plots and histograms in Figure 3 demonstrate the parameters

α_{1}

and

α_{2}

perform stationary and follow normal distribution.

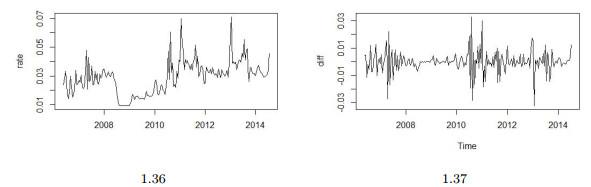
Figure 3 Historical trace and first-order difference of SHIBOR with maturity 7 days

Full size|PPT slide

Table 3 Historical trace and first-order difference of SHIBOR with maturity 7 days

Mean	SD	Maximum	Minimum	Skewness	Kurtosis
0.0291	0.0113	0.0711	0.0093	0.4972	0.9482

Table 4 Estimation via PMCMC

Regime 1	α₁	β₁	σ₁	γ₁	λ₁	μ₁	η₁	p
Mean	0.0127	0.5332	0.0542	0.5699	0.3274	0.0122	0.0056	0.8765
SD	0.0038	0.1034	0.0126	0.0824	0.1987	0.0061	0.0013	0.0494
Regime 2	α₂	β₂	σ₂	γ₂	λ₂	μ₂	η₂	p
Mean	0.0005	0.9474	0.0540	1.0770	0.5315	0.0015	0.0037	0.9174
SD	0.0003	0.0214	0.0127	0.1044	0.1319	0.0009	0.0005	0.0303

Figure 4 Trace plots, histograms and ACF of $α_{1}$ and $α_{2}$

Full size|PPT slide

From the results of parameter estimation, we can see the estimates in regime 1 are bigger commonly than those in regime 2. The economic interpretation of regime switching can account for this phenomenon. Regimes represent business cycle. That is the regime switching that reflects the change of economic environment in models. The difference between regime 1 and 2 suggests that interest rates move more acutely in regime 1 than 2. It is valid for interest rates to behave differently in different regimes, and the results are effective.

5 Conclusion

This paper implements PMCMC method in the term structure of interest rates under Markov regime switching and jumps. The empirical part introduces a Poisson jump component and regime switching to construct the complex state-space models. It is difficult to estimate parameters by using other methods such as maximum likelihood estimate method and Kalman Filter method. The PMCMC algorithm has powerful advantage in tackling nonlinear and non-Gaussian for state-space models. Moreover, it can be implemented conveniently by coding. Both results from simulation and empirical results show that the algorithm is valid and feasible. The PMCMC method can also be applied to more sophisticated state-space models, and enhance efficiency.

References

Publishing order | Descend order by publishing year | Descend order by cited within

1	Bolstad W M. Understanding computational Bayesian statistics. New York: Wiley, 2010. Cited in this article [1]

2	Chorin A J, Morzfeld M, Tu X M. State-space models applications in economics and finance. Statistics and Econometrics for Finance, Springer, 2013, 63- 88.

3	Crisan D, Doucet A. A survey of convergence results on particle filtering methods for practitioners. IEEE Transactions on Signal Processing, 2002, 50, 736- 746. https://doi.org/10.1109/78.984773

4	DelMoral P, Doucet A, Jasra A. On adaptive resampling procedures for sequential Monte Carlo methods. Bernoulli, 2012, 18, 252- 278.

5	Douc R, Moulines E. Limit theorems for weighted samples with applications to sequential Monte Carlo methods. The Annals of Statistics, 2008, 36, 2344- 2376. https://arxiv.org/abs/math/0507042 Cited in this article [1]

6	Gordon N J, Salmond D J, Smith A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. Radar and Signal Processing, IEEE Proceedings F, 1993, 140 (2): 107- 113. https://doi.org/10.1049/ip-f-2.1993.0015 Cited in this article [1]

7	Carpenter J, Clifford P, Fearnhead P. An improved particle filter for nonlinear problems. Radar, Sonar and Navigation, IEE Proceedings, 1999, 146, 2- 7. https://doi.org/10.1049/ip-rsn:19990255 Cited in this article [1]

8	Liu J S, Chen R. Sequential Monte Carlo methods for dynamic systems. Journal of American Statistical Association, 1998, 93, 1032- 1044. https://doi.org/10.1080/01621459.1998.10473765 Cited in this article [1]

9	Doucet A, Godsill S, Andrieu C. On sequential Monte Carlo sampling methods for Bayesian filtering. Statistics and Computing, 2000, 10, 197- 208. https://doi.org/10.1023/A:1008935410038 Cited in this article [1]

10	Doucet A, Johansen A M. A tutorial on particle filtering and smoothing: Fifteen years later. Handbook of Nonlinear Filtering, 2011. Cited in this article [1]

11	Geweke J, Tanizaki H. Bayesian estimation of state-space model using the Metropolis-Hastings algorithm within Gibbs sampling. Computational Statistics & Data Analysis, 2001, 37 (2): 151- 170. https://www.sciencedirect.com/science/article/pii/S0167947301000093

12	Lopes H F, Tsay R S. Particle filters and Bayesian inference in financial econometrics. Journal of Forecasting, 2011, 30, 196- 209.

13	Metropolis N, Rosenbluth A W, Rosenbluth M N, et al. Equation of state calculations by fast computing machines. Journal of Chemical Physics, 1953, 21, 1078- 1092. Cited in this article [1]

14	Pitt M K, Shephard N. Filtering via simulation: Auxiliary particle filters. Journal of American Statistical Association, 1999, 94 (446): 590- 599. https://doi.org/10.1080/01621459.1999.10474153 Cited in this article [1]

15	Zeng Y, Wu S. State-Space Models applications in economics and finance. Statistics and Econometrics for Finance, Springer, 2013. Cited in this article [1]

16	Storvik G. Particle filters in state space models with the presence of unknown static parameters. IEEE: Transactions of Signal Processing, 2002, 50, 281- 289. https://doi.org/10.1109/78.978383

17	Xiong J, Zeng Y. A branching particle approximation to the filtering problem with counting process observations. Statistical Inference for Stochastic Processes, 2011, 14, 111- 140. https://doi.org/10.1007/s11203-011-9053-3 Cited in this article [1]

18	Johannes M, Polson N, Stroud J. Optimal filtering of jump diffusions: Extracting latent states from asset prices. Review of Financial Studies, 2009, 22 (7): 2559- 2599. Cited in this article [1]

19	Malik S, Pitt M K. Particle filters for continuous likelihood evaluation and maximisation. Journal of Econometrics, 2011, 165 (2): 190- 209. https://doi.org/10.1016/j.jeconom.2011.07.006 Cited in this article [1]

20	Carvalho C M, Lopes H F. Simulation-based sequential analysis of Markov switching stochastic volatility models. Computational Statistics & Data Analysis, 2007, 51 (9): 4526- 4542. Cited in this article [1]

21	Rios M P, Lopes H F. The extended Liu and west filter: Parameter learning in Markov switching stochastic volatility models. Chapter 2, in this volume, 2013. Cited in this article [1]

22	Christoffersen P, Jacobs K, Mimouni K. Volatility dynamics for the S & P 500: Evidence from realized volatility, daily returns, and option prices. Review of Financial Studies, 2010, 23, 3141- 3189. https://doi.org/10.1093/rfs/hhq032 Cited in this article [1]

23	Fernández-Villaverde J, Rubio-RamÍrez J F. Estimating macroeconomic models: A Likelihood Approach. Review of Economic Studies, 2007, 74 (4): 1059- 1087. https://doi.org/10.1111/j.1467-937X.2007.00437.x Cited in this article [1]

24	An S, Schorfheide F. Bayesian analysis of DSGE models. Econometric Reviews, 2007, 26 (2-4): 113- 172. https://doi.org/10.1080/07474930701220071 Cited in this article [1]

25	Sarkka S, Solin A, Hartikainan J. Spatiotemporal learning via infinite-dimensional Bayesian filtering and smoothing. IEEE Signal Processing Magazine, 2013, 30 (4): 51- 61. https://doi.org/10.1109/MSP.2013.2246292 Cited in this article [1]

26	Zeng Y. A partially observed model for micromovement of asset prices with Bayes estimation via filtering. Mathematical Finance, 2003, 13, 411- 444. https://doi.org/10.1111/1467-9965.t01-1-00022 Cited in this article [1]

27	Andrieu C, Doucet A, Holenstein R. Particle Markov chain Monte Carlo methods. Journal of the Royal Statistical Society, 2010, 72, 269- 342. https://doi.org/10.1111/j.1467-9868.2009.00736.x Cited in this article [1]

28	Wu S, Zeng Y. Affine regime-switching models for interest rate term structure. Mathematics of Finance, 2004, 351, 375- 386. Cited in this article [1]

29	Wu S, Zeng Y. A general equilibrium model of the term structure of interest rates under regime-switching risk. International Journal of Theoreticaland Applied Finance, 2005, 8, 839- 869. https://doi.org/10.1142/S0219024905003323 Cited in this article [1]

30	Wu S, Zeng Y. The term structure of interest rates under regime shifts and jumps. Economics Letters, Elsevier, 2006, 93, 215- 221. https://doi.org/10.1016/j.econlet.2006.05.006 Cited in this article [1]

Funding

National Natural Science Foundation of China(71471075)

Fundamental Research Funds for the Central University(19JNLH09)

Humanities and Social Sciences Foundation of Ministry of Education, China(14YJAZH052)

PDF(826 KB)

207

Accesses

Citation

Detail

Sections

Recommended

Received	Accepted	Published
2018-09-19	2019-03-15	2020-04-25
Issue Date
2020-04-25

Please choose a citation manager

Content to export

Abstract

Key words

Cite this article

1 Introduction

2 Particle MCMC Algorithm

3 Simulation Study

3.1 A Non-Linear State Space Model

3.2 The Regime-Switching Model

Figure 1 Trace plots, scatter plots and ACF of the parameters $σ_{v}$ and $σ_{w}$

3.3 The Results via PMCMC

Table 1 The comparison between APF and PF under N

Figure 2 Trace plots and ACF of parameters for PF and APF

Table 2 Estimation via PMCMC

4 Empirical Study: Jump-diffusion Model with Regime

Figure 3 Historical trace and first-order difference of SHIBOR with maturity 7 days

Table 3 Historical trace and first-order difference of SHIBOR with maturity 7 days

Table 4 Estimation via PMCMC

Figure 4 Trace plots, histograms and ACF of $α_{1}$ and $α_{2}$

5 Conclusion

{{custom_sec.title}}

{{custom_sec.title}}

References

{{custom_fnGroup.title_en}}

Footnotes

Funding

Share

模态框（Modal）标题

Please choose a citation manager

Content to export

Abstract

Key words

Cite this article

1 Introduction

2 Particle MCMC Algorithm

3 Simulation Study

3.1 A Non-Linear State Space Model

3.2 The Regime-Switching Model

Figure 1 Trace plots, scatter plots and ACF of the parameters σv and σw

3.3 The Results via PMCMC

Table 1 The comparison between APF and PF under N

Figure 2 Trace plots and ACF of parameters for PF and APF

Table 2 Estimation via PMCMC

4 Empirical Study: Jump-diffusion Model with Regime

Figure 3 Historical trace and first-order difference of SHIBOR with maturity 7 days

Table 3 Historical trace and first-order difference of SHIBOR with maturity 7 days

Table 4 Estimation via PMCMC

Figure 4 Trace plots, histograms and ACF of α1 and α2

5 Conclusion

{{custom_sec.title}}

{{custom_sec.title}}

References

{{custom_fnGroup.title_en}}

Footnotes

Funding

Figure 1 Trace plots, scatter plots and ACF of the parameters $σ_{v}$ and $σ_{w}$

Figure 4 Trace plots, histograms and ACF of $α_{1}$ and $α_{2}$