Correlation Analysis of Stock Market and Fund Market Based on M-Copula-EGARCH-M-GED Model

Ruihua WANG; Hongjun WANG

doi:10.21078/JSSI-2020-240-13

PDF(274 KB)

Journal of Systems Science and Information ›› 2020, Vol. 8 ›› Issue (3) : 240-252. DOI: 10.21078/JSSI-2020-240-13

Correlation Analysis of Stock Market and Fund Market Based on M-Copula-EGARCH-M-GED Model

Author information +

History +

Abstract

In this paper, M-Copula is used to analyze the correlation between Shanghai Composite Index and Shanghai Fund Index. By analyzing the characteristics of the logarithmic yields sequence of two samples, the marginal distribution model is established by using EGARCH-M-GED model. According to the correlation between two logarithmic yields sequence, the M-Copula model is selected to model its correlation structure, and its parameters are estimated by EM algorithm. Because MCopula combines characteristics of different Copulas, it has more flexible distribution forms and more prominent ability to describe the fat tails and correlation characteristics of data, and more importantly, the effect is better than single Copula.

Key words

M-Copula / EGARCH-M-GED / EM algorithm / correlation

Cite this article

EndNote

Ris (Procite)

Bibtex

Download Citations

Ruihua WANG , Hongjun WANG. Correlation Analysis of Stock Market and Fund Market Based on M-Copula-EGARCH-M-GED Model. Journal of Systems Science and Information, 2020, 8(3): 240-252 https://doi.org/10.21078/JSSI-2020-240-13

1 Introduction

The emergence of economic globalization and financial integration has brought global financial markets closer together, and accelerated spread and transmission of crises and risks among financial markets. The rapid development of financial market makes its internal relationship more and more complex. Correlation is an important part of quantitative analysis of financial market related structure, and it is also a central issue in financial risk analysis.

In the traditional risk management, Pearson correlation coefficient method and Granger causality analysis method are used to describe and measure the correlation between sequences, but these methods have some drawbacks and limitations. For example, the Pearson correlation coefficient between sequences can only measure linear correlation and requires a limited variance. However, most of yields sequences of financial assets presented with fat tails, variance may not exist, so Pearson correlation coefficients can not be used to reflect the relevance of such data. Furthermore, Pearson correlation coefficient can only describe correlation pattern between sequences, but can not capture relevant features of tails of sequences. And the Pearson correlation coefficient method usually needs to assume that joint distribution obeys normal distribution or

t

distribution, and requires each marginal distribution function to be of the same type. But such assumptions may not be true in many cases.

Calculating a correlation analysis, we need to know density function of joint distribution of sequences. When using Copula^[1] to construct joint distribution, the joint distribution is not only subject to the constraint that marginal distribution belongs to same distribution type, but also distribution function of single sequence and dependent structure between sequences can be studied separately, so the application of Copula is more flexible. Since Embrachts^[2] introduced Copula into financial risk management, it has become a powerful research tool in this field because of its special advantages in analyzing relevance. Many scholars have also made many meaningful contributions in this field. Durrleman^[3] gave a few methods for choice of Copulas in financial modeling, Li^[4] applied Copula function method to study of default correlation, Jaworski^[5] gave a comprehensive introduction to the theory and application of Copula, Rodriguez^[6] used the Copula method to measure financial contagion, Huang^[7] estimated the risk value of portfolio using conditional Copula-GARCH method, Aloui^[8] studied the conditional dependence structure of oil price and exchange rate by Copula-GARCH method, Kim^[9] analyzed direction dependence based on asymmetric Copula regression model, Jondeau^[10] applied the condition-dependent Copula-GARCH model to international stock market research, many follow-up scholars have carried out more in-depth research and application.

Since Hu^[11] first proposed a mixture Copula(M-Copula) model in his article, M-Copula has more comprehensive reflection of correlation between sequences, because M-Copula combines advantages of each single Copula in its components. Therefore, M-Copula has attracted attention of many researchers. Ouyang^[12] studied the dependence based on M-Copula model and its application in the risk management, Ignatieva^[13] analyzed the Australian electricity market spot price dependent model and risk management applications with M-Copula, Harb^[14] uses M-Copula to price CDS spread adjusted by credit valuation.

The parameters of Copula model can be estimated by traditional methods such as moment estimation and maximum likelihood estimation. Shih^[15] deduced the correlation parameters of copula model for binary survival data, Chen^[16] estimates the semi-parametric time series model based on Copula, Joe^[17] studied the asymptotic efficiency of two-stage estimation method based on the Copula model. However, M-Copula model is complex in structure and usually has no analytic solutions by using likelihood method. In recent years, some scholars have used optimization algorithms to estimate the parameters of M-Copula model. Liu^[18] improved and tested the maximum likelihood estimation iteration (fixed point) algorithm based on Copula model, Zhang^[19] used a conventional expectation maximization algorithm to estimate the parameters of the mixed connection function effectively.

Based on the inspiration of the previous article, this paper will be based on the M-Copula-EGARCH-M-GED model analysis, take Composite index and fund index of Shanghai Stock Exchange as an example to analyze the correlation between Shanghai Stock Exchange and fund market. The parameters of the M-Copula model are estimated by EM algorithm.

2 Establishment of Model

2.1 Correlation Theory of Copula Function

Theorem 1

(

Sklar's theorem

(1959)

, see [20]) Let H be a joint distribution function with margins F and G. Then there exists a copula C such that for all $x, y i n \bar{R}$ .

H (x, y) = c (F (x), G (y)) .

(1)

F

and

G

are continuous, then

C

is unique; otherwise,

C

is uniquely determined on. Conversely, if

C

is a Copula and

F

and

G

are distribution function, then the function

H

defined by Equation (1) is a joint distribution function with margins

F

and

G

Sklar's theorem reveals the role of Copula function in linking joint distribution and marginal distribution, which lays a theoretical foundation for the application of Copula function in financial analysis.

M-Copula is a linear convex combination of Copula functions, which is more flexible than single Copula function. Because it combines the advantages of component Copula, it can simultaneously display the ability of each Copula to describe different related features of sequence. So as to enhance its strengths and avoid its weaknesses, and achieve better results in capturing more complex related features. The general form of the M-Copula model is as follows in Equation (2), if

C_{1}

C_{2}

\dots

C_{n}

are Copula functions, then their convex combination

C (u, v; θ) = \sum_{i = 1}^{n} λ_{i} C_{i} (u, v; φ),

(2)

also a Copula function, where

\sum_{i = 1}^{n} λ_{i} = 1, λ_{i} \geq 0

is the weight parameter, is the relevant parameter.

In the third section of empirical study, by analyzing the selected data, select Gumbel, Clayton, and Frank function in Archimedes Copula, and the M-Copula model by linear combination equation (3), the correlation between two yields sequence is studied and compared.

M C_{3} (u, v; θ) = w_{G} C_{G} (u, v; α) + w_{C l} C_{C l} (u, v; β) + w_{F} C_{F} (u, v; λ),

(3)

in which

w_{G}

w_{C l}

w_{F}

represents the weight of each Gumbel, Clayton and Frank function weighting coefficients, also is the function M-Copula weight parameter (

w_{G}

w_{C l}

w_{F}

2.2 Copula-EGARCH-M-GED Model

Copula model building process, select an appropriate marginal distribution is a key step. Most of the conditional distributions of financial time series have the characteristics of time-varying fluctuations, clustering, skewness, spikes and fat tails. The ARCH model can characterize these properties, and thus can better describe condition distribution of financial yields sequences, which is conducive to improving the accuracy of Copula model, so as to achieve better modeling results.

The conditional distribution of financial time series often has the characteristics of sharp peaks and fat tails. The fat tail characteristics of

t

distribution and GED distribution (generalized error distribution) perform well when characterizing the above characteristics of data. The GARCH model has a strong generalization ability, and the ability to describe time series volatility is better than the ARCH model. The exponential GARCH (EGARCH) model proposed by Nelson^[21] overcomes the non-negative limitation of parameters in the linear GARCH(LGARCH) model, and overcomes the shortcomings of the LGARCH model that it is difficult to judge persistence of the conditional variance fluctuation source. The GARCH-M model was proposed by Engle^[22], it is the fact that the GARCH model takes into account the fact that the conditional variance changes with time. The GARCH model is extended so that the conditional variance can directly affect the mean of the returns. The economic significance of the GRACH-M model is very obvious and has been widely recognized. Therefore, the EGARCH-M-GED model is used to fit the sample yield sequence. The binary Copula-EGARCH(1, 1)-M-GED form is as follows:

\begin{aligned} R_{n, t} = μ_{n} + δ_{n} h_{n, t}^{2} + ε_{n, t}, \\ ε_{n, t} = h_{n, t} ξ_{n, t}, \\ \ln (h_{n, t}^{2}) = {\bar{ω}}_{n} + γ_{n} [\frac{ε_{n, t - 1}}{h_{n, t - 1}}] + α_{n} | \frac{ε_{n, t - 1}}{h_{n, t - 1}} | + β_{n} \ln (h_{n, t - 1}^{2}), \\ (ξ_{1 t}, ξ_{2 t}) \sim C (F_{ξ_{1}} (X), F_{ξ_{2}} (Y)), n = {1, 2}, t = {1, 2, \dots, T}, \\ ξ_{n t} \sim i . i . d . (0, 1), (ξ_{1 t}, ξ_{2 t}) \sim i . i . d . (0, 1); ξ_{1 t} \sim G E D_{1}, ξ_{2 t} \sim G E D_{2} . \end{aligned}

(4)

The standard deviations of the marginal distribution functions

F_{ξ_{1}} (x) = \int_{- \infty}^{x} \frac{v_{1} \cdot \exp {- \frac{1}{2} {| \frac{t}{λ_{1}} |}^{v_{1}}}}{λ_{1} 2^{1 + \frac{1}{v_{1}}} Γ (\frac{1}{v_{1}})} d t, F_{ξ_{2}} (y) = \int_{- \infty}^{y} \frac{v_{2} \cdot \exp {- \frac{1}{2} {| \frac{t}{λ_{2}} |}^{v_{2}}}}{λ_{2} 2^{1 + \frac{1}{v_{2}}} Γ (\frac{1}{v_{2}})} d t

are respectively

ξ_{1}, ξ_{2}

the thickness parameters of the tail are respectively

V_{1}

and

V_{2}

, and the shape parameters are respectively

λ_{1} = [2^{- \frac{2}{v_{1}}} \cdot \frac{Γ (\frac{1}{v_{1}})}{Γ (\frac{3}{v_{1}})}]^{\frac{1}{2}}

and

λ_{2} = [2^{- \frac{2}{v_{2}}} \cdot \frac{Γ (\frac{1}{v_{2}})}{Γ (\frac{3}{v_{2}})}]^{\frac{1}{2}} .

2.3 Expectation Maximization Algorithm

EM algorithm (expectation maximization algorithm) is not only an iterative optimization strategy, but also a data addition algorithm. In 1977, EM algorithm was summarized by Dempster^[23] for maximum likelihood estimation or maximum posterior probability estimation of parameters of probability model with latent variables. The most commonly used method to obtain the estimation of model parameters from sample observation sequence is to maximize logarithmic likelihood function of model distribution. However, in some cases, the observed data has unobserved hidden variables, and the estimated results of model parameters cannot be directly obtained by maximizing log-likelihood function. In this case, the EM algorithm can be considered. Each iteration of the EM algorithm consists of two steps: Expectations are computed in step E and maximization of likelihood functions in step M. The hidden variables and model parameters are iteratively updated until the convergence, the estimated results of model parameters can be obtained.

In the empirical research, the yield series

(u_{1}, v_{1}), (u_{2}, v_{2}), \dots, (u_{T}, v_{T})

where

T = 1402

its joint distribution function is formula (3) M-Copula. That is

P (u, v | θ) = M C_{3} (u, v; θ) = w_{G} C_{G} (u, v; α) + w_{C l} C_{C l} (u, v; β) + w_{F} C_{F} (u, v; λ)

Parameters

θ = (w_{G}, w_{C l}, w_{F}; α, β, λ)

, Estimated by EM algorithm. In order to discuss concisely,

w_{G}, w_{C l}, w_{F}

is recorded as

w_{1}, w_{2}, w_{3}, C_{G}, C_{C l}, C_{F}

and

c_{G}, c_{C l}, c_{F}

C_{1}, C_{2}, C_{3}

and

c_{1}, c_{2}, c_{3}

respectively.

Implicit variables are introduced to obtain logarithmic likelihood functions for complete data: The probability distribution model of yield series

(u_{i}, v_{i}), i = 1, 2, \dots, T

is the model equation (3), but it is unknown which sub-model

C_{1}, C_{2}, C_{3}

a pair of

(u_{i}, v_{i})

belongs to. Therefore, variable

γ_{i k}

is introduced to reflect the sub-model of yield series

(u_{i}, v_{i})

, which is defined as follows:

γ_{i k} = {\begin{cases} 1, & t h e i - p a i r y i e l d s e r i e s c o m e s f r o m t h e k - s u b - m o d e l, \\ 0, & o t h e r w i s e, \end{cases}

i = 1, 2, \dots, T; k = 1, 2, 3.

The yield series

(u_{i}, v_{i}), i = 1, 2, \dots, T

is known, and after adding the unobserved data

γ_{i k}

, the complete data is

(u_{i}, v_{i}, γ_{i 1}, γ_{i 2}, γ_{i 3}), i = 1, 2, \dots, T .

The likelihood function of complete data is obtained:

\begin{array}{rcl} P (u, v, γ | θ) & = & \prod_{i = 1}^{T} P (u_{i}, v_{i}, γ_{i 1}, γ_{i 2}, γ_{i 3} | θ) \\ = & \prod_{k = 1}^{3} {\prod_{i = 1}^{T} [w_{k} c_{k} (u_{i}, v_{i} | θ_{k})]}^{γ_{i k}} \\ = & \prod_{k = 1}^{3} {w_{k}^{n_{k}} \prod_{i = 1}^{T} [c_{k} (u_{i}, v_{i} | θ_{k})]}^{γ_{i k}}, \end{array}

(5)

the

n_{k} = \sum_{i = 1}^{T} γ_{i k}, \sum_{k = 1}^{3} n_{k} = T

Thus, the logarithmic likelihood function of complete data is

\log P (u, v, γ | θ) = \sum_{k = 1}^{3} {n_{k} \log w_{k} + \sum_{i = 1}^{T} γ_{i k} \log c_{k} (u_{i}, v_{i} | θ_{k})} .

(6)

Step E Computing expectations for logarithmic likelihood function of complete data with respect to implicit variable

γ_{i k}

, under the condition that

(u, v)

and the parameter

θ^{(i)}

are known by the

i^{t h}

estimation. It is recorded as a Q function.

\begin{array}{rcl} Q (θ, θ^{(i)}) & = & E [\log P (u, v, γ | θ) | u, v, θ^{(i)}] \\ = & E {\sum_{k = 1}^{3} {n_{k} \log w_{k} + \sum_{i = 1}^{T} γ_{i k} \log c_{k} (u_{i}, v_{i} | θ_{k})} | u, v, θ^{(i)}} \\ = & \sum_{k = 1}^{3} {n_{k} \log w_{k} + \sum_{i = 1}^{T} (E γ_{i k}) \log c_{k} (u_{i}, v_{i} | θ_{k})} . \end{array}

(7)

Calculate

E (γ_{i k} | u, v, θ)

and mark

{\hat{γ}}_{i k}

\begin{array}{rcl} {\hat{γ}}_{i k} & = & E (γ_{i k} | u, v, θ) = P (γ_{i k} = 1 | u, v, θ) \\ = & \frac{P (γ_{i k} = 1, u_{i}, v_{i} | θ)}{\sum_{k = 1}^{3} P (γ_{i k} = 1, u_{i}, v_{i} | θ)} \\ = & \frac{w_{k} c_{k} (u_{i}, v_{i} | θ_{k})}{\sum_{k = 1}^{3} w_{k} c_{k} (u_{i}, v_{i} | θ_{k})}, i = 1, 2, \dots, T; k = 1, 2, 3. \end{array}

(8)

{\hat{γ}}_{i k}

denotes the probability that the first i-pair sequence belongs to the sub-model k, so it is called the response of the sub-model k to the yield sequence

(u_{i}, v_{i}) .

The

{\hat{γ}}_{i k} = E γ_{i k}

substitution Formula (2.7) is available.

Q (θ, θ^{(i)}) = \sum_{k = 1}^{3} {n_{k} \log w_{k} + \sum_{i = 1}^{T} {\hat{γ}}_{i k} \log c_{k} (u_{i}, v_{i} | θ_{k})} .

(9)

Step M Calculate the maximum value of function

Q (θ, θ^{(i)})

θ .

The model parameters of iteration in the new round are as follows

θ^{(i + 1)} = \arg max_{θ} Q (θ, θ^{(i)})

{\hat{w}}_{k}, k = 1, 2, 3, \hat{α}, \hat{β}, \hat{λ},

is used to represent the parameters of

θ^{(i + 1)} .

The results are as follows:

\begin{array}{rcl} \hat{α} = a r g m a x \sum_{i = 1}^{N} {\hat{γ}}_{i 1} c_{1} (u_{i}, v_{i} | α_{k}), \\ \hat{β} = \arg max \sum_{i = 1}^{N} {\hat{γ}}_{i 2} c_{2} (u_{i}, v_{i} | β_{k}), \\ \hat{λ} = \arg max \sum_{i = 1}^{N} {\hat{γ}}_{i 3} c_{3} (u_{i}, v_{i} | λ_{k}), \\ {\hat{w}}_{k} = \frac{\sum_{i = 1}^{N} {\hat{γ}}_{i k}}{N}, k = 1, 2, 3. \end{array}

(10)

The E-step and M-step are iterated repeatedly until convergence, and finally the estimation results of parameters are obtained.

2.4 Testing Copula Model

Copula goodness-of-fit test is the criterion to judge and measure the excellent modeling effect of Copula model, Berg^[24] summarized and compares several methods of Copula goodness of fit test. In this paper, two methods are used to test the copula model.

Distance criterion The empirical distribution function is used as the simulation value of the real Copula function, comparison of the estimated Copula function and real function Copula distance

d^{2}

. The square Euclidean distance between Copula function and empirical Copula function is defined as:

d^{2} = \sum_{i = 1}^{n} {| {\hat{C}}_{n} (u_{i}, v_{i}) - C (u_{i}, v_{i}) |}^{2} .

(11)

The smaller the value of

d^{2}

is, the better the fitting effect will be.

Statistical Mis a distribution-dependence test statistic introduced by Hu^[11]. It is used to evaluate the goodness of fit Copula function. It is based on the probabilistic integral transformation of the observation sequence

{X_{t}}

and

{Y_{t}}, t = 1, 2, \dots, n

to obtain a new uniform sequence

{U_{t}}

and

{V_{t}}, t = 1, 2, \dots, n

and to construct a table

G

containing

k \times k

cells. The cella in row

i

and column

j

in the table are denoted as

G (i, j), i, j = 1, 2, \dots, k

. For any point

(u_{t}, v_{t})

\frac{i - 1}{k} \leq u_{t} < \frac{i}{k}

and

\frac{j - 1}{k} \leq v_{t} < \frac{j}{k}

, then

(u_{t}, v_{t}) \in G (i, j) .

G (i, j)

represents a set of probability whose lower bound is

[\frac{i - 1}{k}, \frac{j - 1}{k}]

and upper bound is

(\frac{i}{k}, \frac{j}{k}) .

A_{i j}

denotes the number of actual observation points in cell

G (i, j),

B_{i j}

denotes the number of points in cell

G (i, j)

predicted by Copula model. The

χ^{2}

-test statistic M, which evaluates the goodness of fit of Copula function, is expressed as:

M = \sum_{i = 1}^{k} \sum_{j = 1}^{k} \frac{{(A_{i j} - B_{i j})}^{2}}{B_{i j}} .

(12)

Statistical M obeys

χ^{2}

distribution with degree of freedom

(k - 1)^{2}

. In this paper,

k = 20

is selected according to the total number of observation points.

3 Empirical Analysis

3.1 Descriptive Statistical Analysis of Sample Data

This paper selects the Shanghai Composite Index (SHCI) and the fund index (SHFI) issued by the Shanghai Stock Exchange in China's financial market to represent the stock and fund markets for correlation analysis. Taking the daily closing price as a sample, the price

{P_{t}}

is taken as the index closing price on the

t^{t h}

day day, and the yield is defined as

R_{t} = 100 (\ln P_{t} - \ln P_{t - 1})

. The selected data period is from January 4, 2013 to October 11, 2018, with a total of 1402 observations.

Time series Figure 1 and descriptive statistical results Table 1 shows that logarithmic yields sequences of composite index and fund index have the characteristics of general financial time series with fluctuation clusters, spikes and fat tails. Moreover, the test results of the normality test JB statistic^[25] indicate that normal distribution hypothesis is rejected.

Figure 1 Time series diagram of logarithmic return rate

Full size|PPT slide

Table 1 Descriptive statistical results

index	Max	Min	Mean	std.Dev	Skewness	Kurtosis	JB
SHCI	6.3329	$-$ 9.4791	0.0133	1.4799	$-$ 0.7340	6.6969	2755
SHFI	6.5422	$-$ 7.5514	0.0247	1.0434	$-$ 0.8390	11.0702	7344.6

3.2 Time Series Analysis and Modeling

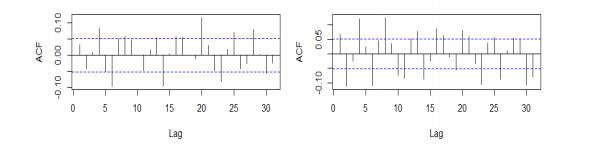
The ACF graph of the two logarithmic rate of return series in Figure 2 shows that there is basically no autocorrelation. The PACF plot of the square of the logarithmic return series in Figure 3 shows that there is a significant autocorrelation in the high-order lag period. And the

P

value of the Ljung-Box test of the square of the two return series is small

(2 \times 10^{- 16})

, so there is obvious ARCH effect.

Figure 2 ACF of logarithmic return series of composite index (left) and fund index (right)

Full size|PPT slide

Figure 3 PACF of the square of logarithmic return series of composite index and fund index

Full size|PPT slide

The sample data was fitted using the EGARCH(1, 1)-M-GED model. The Q-Q diagram of the fitting results is shown in Figure 4. It can be seen that the EGARCH(1, 1)-M-GED model has a good fitting effect on the selected samples.

Figure 4 Q-Q graph of EGARCH-M-GED fitting results for logarithmic return series of composite index and fund index

Full size|PPT slide

The edge distribution of the return series is modeled by EGARCH(1, 1)-M-GED, and Tables 2 and 3 are the estimation and test results.

Table 2 Parameter estimation table of shanghai composite index return sequence

Parameter	Estimate	std.Error	$T$ value	$P r (> \| t \|)$
$μ$	0.0245	0.0127	1.9216	0.0547
$δ$	$-$ 0.0179	0.0118	$-$ 1.5137	0.1301
$ω$	0.0022	0.0030	0.7126	0.4761
$γ$	0.0105	0.0147	0.7115	0.4768
$α$	0.1431	0.0091	15.70	0.0000
$β$	0.9933	0.0000	463290	0.0000
$ν$	1.0812	0.0513	21.08	0.0000

Table 3 Parameter estimation table of ShangHai fun index return sequence

Parameter	Estimate	std.Error	$T$ value	$P r (> \| t \|)$
$μ$	0.0145	0.0023	6.2501	0.0000
$δ$	$-$ 0.0014	0.0023	$-$ 0.5818	0.5607
$ω$	$-$ 0.0049	0.0053	$-$ 0.9153	0.3600
$γ$	$-$ 0.0035	0.0208	$-$ 0.1707	0.8645
$α$	0.2608	0.0302	8.6264	0.0000
$β$	0.9939	0.0018	539.49	0.0000
$ν$	1.0066	0.0497	20.26	0.0000

From Table 2 and Table 3, we know that

γ \neq 0

, which shows that both the Shanghai Stock Market and the fund market have leverage effect; and

α + β

is greater than 1, which shows that the current information in the model is very important for predicting future conditional variance. It can be seen that the EGARCH(1, 1)-M-GED model has a good effect on the conditional edge distribution of the fitted sequence. Therefore, it is reasonable to select the EGARCH(1, 1)-M-GED model to describe the conditional edge distribution of the sequence.

3.3 Copula Function Modeling

The scatter plot 5 of the empirical distribution after the residual sequence transformation shows that the tail dependence between the two sequences is strong. Given the frequency distribution histogram 6 corresponding to the above samples, the joint distribution of the two sample return series can be observed. The frequency of the sample at the upper and lower tails is higher and asymmetrical, and the distribution of the lower tail is heavier than that of the upper tail. It can be judged that the

P [Y \leq y | X \leq x]

at the lower end is a non-decreasing function with respect to the variable

X

, and the situation at the upper tail is similar. Therefore, it shows that there is a strong tail correlation at the top and bottom.

Figure 5 Empirical Distribution

Full size|PPT slide

Figure 6 Frequency distribution histogram

Full size|PPT slide

A single Gumbel, Clayton and Frank Copula function is selected for modeling analysis. The parameters in the Copula function are estimated by the method of empirical distribution function in nonparametric kernel density estimation.

Tables 4 show that different Copula models have great differences in the ability to describe the correlation between composite index and fund index, the Euclidean distance square of M-Copula is smaller than that of Archimedes Copula in Table 4, and the M-statistics of M-Copula are significant at the level of 0.05, that is to say, the fitting effect of M-Copula is the best. The weight coefficient of the Gumbel function in M-Copula is the largest, and the weight coefficient of Frank and Clayton is small, indicating that there is an asymmetric tail correlation between yields sequence of composite index and fund index. The estimated values of the relevant parameters indicate that there is a strong positive correlation between composite index and fund index.

Table 4 Parameter estimation results of Copula model

	Copula	Parameter	Likelihood function	$d^{2}$	M
	Gumbel	0.2332	1700.56	0.5370	191.4759(103)
	Clayton	2.0841	1550.67	0.0631	501.3113(122)
	Frank	16.1227	1574.97	0.1646	207.9246(115)
Relational	Gumbel	0.1995	1832.18	0.0372	114.7360*(108)
	Clayton	4.6519
	Frank	5.6218
Weight	Gumbel	0.5693
	Clayton	0.3670
	Frank	0.0637

^* The values in parentheses of statistic M are corresponding degrees of freedom, and ^* is significant at the level of 0.05.

Figure 7 is a frequency distribution diagram of empirical distribution obtained by probability integral transformation of composite index and fund index yields sequences, and the estimated frequency distribution of probability distribution determined by M-Copula. The M-Copula distribution is very close to the empirical distribution, and most of the observation points fall near the main diagonal of

u = v

. This indicates that there is a significant positive correlation between composite index and fund index, which is consistent with the results of estimated parameters of M-Copula. In addition, there is an asymmetric tail-related structure between composite index and fund index.

Figure 7 Frequency distribution of empirical distribution and M-Copula probability distribution

Full size|PPT slide

3.4 Result Analysis

Figure 8 shows a comparison of empirical distribution and frequency distribution of several Copula distributions at

u = v

. The variation of distribution on the main diagonal of

u = v

reflects coordinated movement between financial markets. Four kinds of Copula are better characterize the effect of correlation between two yields sequences in normal times. However, there is a big difference in the correlation between two yields sequences when the tail of the distribution, that is, the extreme event occurs. Gumbel underestimates lower tail and overestimates upper tail, and indicates that correlation between upper tail and tail is stronger, which is contrary to higher correlation between lower tail and the tail of the empirical Copula function distribution. Clayton clearly overestimates the bottom and underestimates upper tail. Frank is underestimated for both upper and lower tails and does not reflect the asymmetric tail correlation between composite index and fund index. M-Copula is very close to the empirical distribution at upper and lower tails, and can accurately capture the correlation between two periods of two yields sequences, which can reflect the correlation pattern between two indexes more realistically.

Figure 8 Comparison of Gumbel, Clayton, Frank and M-copula with empirical distribution

Full size|PPT slide

4 Summary

Although Copula has the property of being able to separate marginal distribution from joint distribution, it provides great convenience in correlation analysis. However, the increasingly complex changes in financial markets make it difficult to accurately describe the relevant structures between markets using single Copula model. In this case, M-Copula is due to its special construction. Combining the characteristics of single Copula model, the form is flexible, and the scope of application is broader, which can portray more complex correlations between financial markets. In this paper, combined with the EGARCH-M-GED model, M-Copula is mainly used to study the correlation between composite index and fund index. A comparative analysis of the correlation between two yields sequences of single Archimedes Copula and M-Copula, the parameters of M-Copula were estimated using EM algorithm. The results of empirical research show that M-Copula can more accurately capture asymmetric tail correlation between two yields sequences.

References

Publishing order | Descend order by publishing year | Descend order by cited within

1	Genest C, Favre A C. Everything you always wanted to know about Copula modeling but were afraid to ask. Journal of Hydrologic Engineering, 2007, 12 (4): 347- 368. https://doi.org/10.1061/(ASCE)1084-0699(2007)12:4(347) Cited in this article [1]

2	Embrechts P, McNeil A, Straumann D. Correlation and dependence in risk management: Properties and pitfalls. Dempsker M. Risk management: Value at Risk and beyond. Cambridge: Cambridge University Press, 2002: 176- 223. Cited in this article [1]

3	Durrleman V, Nikeghbali A, Roncalli T. Which copula is the right one? Working Document. Groupe de Recherche Opérationnelle, Crédit Lyonnais, 2000. Cited in this article [1]

4	Li D X. On default correlation: A Copula function approach. Journal of Fixed Incom, 2000, (3): 43- 54. Cited in this article [1]

5	Jaworski P, Hardle W K, Rychlik T, et al. Copula theory and its applications. New York: Springer, 2009. Cited in this article [1]

6	Rodriguez J C. Measuring financial contagion: A Copula approach. Journal of Empirical Finance, 2007, 14 (3): 401- 403. https://doi.org/10.1016/j.jempfin.2006.07.002 Cited in this article [1]

7	Huang J J, Lee K J, Liang H, et al. Estimating value at risk of portfolio by conditional copula-GARCH method. Insurance Mathematics and Economics, 2009, 45 (3): 315- 324. https://doi.org/10.1016/j.insmatheco.2009.09.009 Cited in this article [1]

8	Aloui R, Aïssa M S B, Nguyen D K, et al. Conditional dependence structure between oil prices and exchange rates: A copula-GARCH approach. Journal of International Money and Finance, 2013, 32 (1): 719- 738. Cited in this article [1]

9	Kim D, Kim J M. Analysis of directional dependence using asymmetric copula-based regression models. Journal of Statistical Computation and Simulation, 2014, 84 (9): 1990- 2010. https://doi.org/10.1080/00949655.2013.779696 Cited in this article [1]

10	Jondeau E, Rockinger M. The Copula-GARCH model of conditional dependencies: An international stock market application. Journal of International Money and Finance, 2006, 25 (5): 827- 853. https://doi.org/10.1016/j.jimonfin.2006.04.007 Cited in this article [1]

11	Hu L. Dependence patterns across financial markets: A mixed copula approach. Applied Financial Economics, 2006, 16 (10): 717- 729. https://doi.org/10.1080/09603100500426515 Cited in this article [2]

12	Ouyang Z S, Liao H, Yang X Q. Modeling dependence based on mixture copulas and its application in risk Management. Applied Mathematics A Journal of Chinese Universities, 2009, 24 (4): 393- 401. https://doi.org/10.1007/s11766-009-2249-2 Cited in this article [1]

13	Ignatieva K, Trück S. Modeling spot price dependence in Australian electricity markets with applications to risk management. Computers and Operations Research, 2015, 66, 415- 433. Cited in this article [1]

14	Harb E, Louhichi W. Pricing CDS spreads with Credit Valuation Adjustment using a mixture copula. Research in International Business and Finance, 2016, 39, 963- 975. Cited in this article [1]

15	Shih J H, Louis T A. Inferences on the association parameter in Copula models for bivariate survival data. Biometrics, 1995, 51 (4): 1384- 1399. https://doi.org/10.2307/2533269 Cited in this article [1]

16	Chen X, Fan Y. Estimation of copula-based semiparametric time series models. Journal of Econometrics, 2006, 130 (2): 307- 335. https://doi.org/10.1016/j.jeconom.2005.03.004 Cited in this article [1]

17	Joe H. Asymptotic efficiency of the two-stage estimation method for copula-based models. Journal of Multivariate Analysis, 2008, 94 (2): 401- 419. Cited in this article [1]

18	Liu Y, Luger R. Efficient estimation of Copula-GARCH models. Computational Statistics and Data Analysis, 2009, 53 (6): 2284- 2297. https://doi.org/10.1016/j.csda.2008.01.018 Cited in this article [1]

19	Zhang Q, Shi X. A mixture Copula bayesian network model for multimodal genomic data. Cancer Informatics, 2017, 16, 117693511770238. https://doi.org/10.1177/1176935117702389 Cited in this article [1]

20	Sklar A. Fonctions de repartition à n dimensions et leurs marges. Publication de I'Institut de Statistique de I'Université de Paris, 1959, 8, 229- 231. Cited in this article [1]

21	Nelson D B. ARCH models as diffusion approximations. Journal of Econometrics, 1990, 45 (1): 7- 38. Cited in this article [1]

22	Engle R E, Bollerslev T. Modeling the persistence of conditional variances. Economic Review, 1986, 5, 81- 87. https://doi.org/10.1080/07474938608800101 Cited in this article [1]

23	Dempster A P, Laird N M, Rubin D B. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, 1977, 39 (1): 1- 38. Cited in this article [1]

24	Berg D. Copula goodness-of-fit testing: An overview and power comparison. European Journal of Finance, 2009, 15 (7-8): 675- 701. https://doi.org/10.1080/13518470802697428 Cited in this article [1]

25	Jarque C M, Bera A K. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Economics Letters, 2006, 6 (3): 255- 259. Cited in this article [1]

Funding

National Natural Science Foundation of China(61573266)

PDF(274 KB)

186

Accesses

Citation

Detail

Sections

Recommended

Abstract
Key words
Cite this article
1 Introduction
2 Establishment of Model
2.1 Correlation Theory of Copula Function
2.2 Copula-EGARCH-M-GED Model
2.3 Expectation Maximization Algorithm
2.4 Testing Copula Model
3 Empirical Analysis
3.1 Descriptive Statistical Analysis of Sample Data
Figure 1 Time series diagram of logarithmic return rate
Table 1 Descriptive statistical results
3.2 Time Series Analysis and Modeling
Figure 2 ACF of logarithmic return series of composite index (left) and fund index (right)
Figure 3 PACF of the square of logarithmic return series of composite index and fund index
Figure 4 Q-Q graph of EGARCH-M-GED fitting results for logarithmic return series of composite index and fund index
Table 2 Parameter estimation table of shanghai composite index return sequence
Table 3 Parameter estimation table of ShangHai fun index return sequence
3.3 Copula Function Modeling
Figure 5 Empirical Distribution
Figure 6 Frequency distribution histogram
Table 4 Parameter estimation results of Copula model
Figure 7 Frequency distribution of empirical distribution and M-Copula probability distribution
3.4 Result Analysis
Figure 8 Comparison of Gumbel, Clayton, Frank and M-copula with empirical distribution
4 Summary
References
Funding

Received	Accepted	Published
2019-09-18	2019-11-20	2020-06-25
Issue Date
2020-06-25

Please choose a citation manager

Content to export

Abstract

Key words

Cite this article

1 Introduction

2 Establishment of Model

2.1 Correlation Theory of Copula Function

2.2 Copula-EGARCH-M-GED Model

2.3 Expectation Maximization Algorithm

2.4 Testing Copula Model

3 Empirical Analysis

3.1 Descriptive Statistical Analysis of Sample Data

Figure 1 Time series diagram of logarithmic return rate

Table 1 Descriptive statistical results

3.2 Time Series Analysis and Modeling

Figure 2 ACF of logarithmic return series of composite index (left) and fund index (right)

Figure 3 PACF of the square of logarithmic return series of composite index and fund index

Figure 4 Q-Q graph of EGARCH-M-GED fitting results for logarithmic return series of composite index and fund index

Table 2 Parameter estimation table of shanghai composite index return sequence

Table 3 Parameter estimation table of ShangHai fun index return sequence

3.3 Copula Function Modeling

Figure 5 Empirical Distribution

Figure 6 Frequency distribution histogram

Table 4 Parameter estimation results of Copula model

Figure 7 Frequency distribution of empirical distribution and M-Copula probability distribution

3.4 Result Analysis

Figure 8 Comparison of Gumbel, Clayton, Frank and M-copula with empirical distribution

4 Summary

{{custom_sec.title}}

{{custom_sec.title}}

References

{{custom_fnGroup.title_en}}

Footnotes

Funding

Share

模态框（Modal）标题

Please choose a citation manager

Content to export

Abstract

Key words

Cite this article

1 Introduction

2 Establishment of Model

2.1 Correlation Theory of Copula Function

2.2 Copula-EGARCH-M-GED Model

2.3 Expectation Maximization Algorithm

2.4 Testing Copula Model

3 Empirical Analysis

3.1 Descriptive Statistical Analysis of Sample Data

Figure 1 Time series diagram of logarithmic return rate

Table 1 Descriptive statistical results

3.2 Time Series Analysis and Modeling

Figure 2 ACF of logarithmic return series of composite index (left) and fund index (right)

Figure 3 PACF of the square of logarithmic return series of composite index and fund index

Figure 4 Q-Q graph of EGARCH-M-GED fitting results for logarithmic return series of composite index and fund index

Table 2 Parameter estimation table of shanghai composite index return sequence

Table 3 Parameter estimation table of ShangHai fun index return sequence

3.3 Copula Function Modeling

Figure 5 Empirical Distribution

Figure 6 Frequency distribution histogram

Table 4 Parameter estimation results of Copula model

Figure 7 Frequency distribution of empirical distribution and M-Copula probability distribution

3.4 Result Analysis

Figure 8 Comparison of Gumbel, Clayton, Frank and M-copula with empirical distribution

4 Summary

{{custom_sec.title}}

{{custom_sec.title}}

References

{{custom_fnGroup.title_en}}

Footnotes

Funding