Strategic Behavior and Optimization in an Unobservable Constant Retrial Queue with Balking and Set-Up Time

Linlin WANG; Liwei LIU; Zhen WANG; Xudong CHAI

doi:10.21078/JSSI-2020-273-18

PDF(441 KB)

Journal of Systems Science and Information ›› 2020, Vol. 8 ›› Issue (3) : 273-290. DOI: 10.21078/JSSI-2020-273-18

Strategic Behavior and Optimization in an Unobservable Constant Retrial Queue with Balking and Set-Up Time

Author information +

History +

Abstract

An M/M/1 constant retrial queue with balking customers and set-up time is considered. Once the system becomes empty, the server will be turned down to reduce operating costs, and it will be activated only when there is a customers arrives. In this paper, the almost unobservable case is studied, in which the information of the queue length is unavailable, whereas the state of the server can be obtained. Firstly, the steady state solutions are derived and the individual equilibrium strategies are analyzed. In addition, social optimization problems, including cost analysis and social welfare maximization are investigated by using the PSO algorithm. Finally, by appropriate numerical examples, the sensitivity of some main system parameters is shown.

Key words

retrial queue / set-up time / unobservable / equilibrium / PSO algorithm

Cite this article

EndNote

Ris (Procite)

Bibtex

Download Citations

Linlin WANG , Liwei LIU , Zhen WANG , Xudong CHAI. Strategic Behavior and Optimization in an Unobservable Constant Retrial Queue with Balking and Set-Up Time. Journal of Systems Science and Information, 2020, 8(3): 273-290 https://doi.org/10.21078/JSSI-2020-273-18

1 Introduction

In recent years, retrial queueing systems have been widely adopted to model LAN (local area networking) systems. Because in a LAN, a job that can not be disposed at its arrival instant will be translated again in a later time, which consistents with the key thought of retrial queues. Assuming that the waiting space is finite, when the server is idle, new arriving customer will take up the server and accept service immediately. Otherwise if the server is in other states, then arriving customers have to leave the server, but they can join a virtual retrial orbit and wait for retry. So far, there has been vast literature on retrial queuing system. Falin and Templeton^[1] summarized the main methods and results of previous research on retrial queuing system. For interested readers, more details can be found in Artalejo^[2], Gomez-Corral^[3] and Artalejo^[4]. It is worth noting that in the retrial queuing literatures, most of the articles assume that the retrial intervals of customers are independent and follow the exponential distribution with the parameter of

θ

. Under this strategy, the total retrial rate changes with the number of customers in the orbit. While in our model, customers in the orbit follow the first come, first served discipline (FCFS), only the head customer can retry for service after a random time, therefore the retrial rate becomes a constant and is independent of the queue length. Fayolle^[5] first came up with the constant retrial policy to model a telephone exchange system, Later researches can be seen in Falin^[6], Artalejo, Gomez-Corral^[7].

During the past two decades, the game theory has been introduced into the queueing systems. Various queueing models have been studied from the perspective of economics. In equilibrium literature, Naor^[8] first investigated an observable M/M/1 queue under the linear reward-cost structure. He gave the equilibrium balking strategy and proposed that customers could enter the system with social optimal strategy if charged tolls. Edelson and Hildebrand^[9] studied the same model under the assumption that the new arrival customers could not observe the system queue length. Subsequently, many researchers devoted to study and generalize the queueing model, and achieved more results.

In addition, for the set-up time, it was first studied from an economic view by Burnetas and Economou^[10] as a vacation policy. For the sake of costs reduction and energy saving, when the system becomes empty, the server should be turned down and won't be restarted until a customer arrives. Considering to the reality, the opening time of the server should not be ignored. Therefore, regarding the set-up time as a random time subjected to exponential distribution is widely accepted. Zhang and Wang^[11] studied an M/G/1 retrial queue with reserved idle time and setup time. They derived the optimal pricing strategies from the view of the social planner and the server, respectively. However, they take consideration of the general retrial rate, and assume that the information of the queue length and the server's state are unobservable, which are quite different from this paper. Recent results of queueing systems with set-up time can be seen in Yutaka, Yoshitaka, Yutaka, et al.^[12].

The main contribution of this article is the introduction of the set-up time to a constant retrial queue. After the set-up time policy is added, the model becomes more realistic and is firstly studied from an economic view. Closed server will only be activated by an arriving customer and will go through a period of set-up time. Under the almost unobservable condition, we not only derive the customers' equilibrium strategies, but also investigate the social optimization problems respectively from the standpoints of the service provider and the social manager, so that each party in the game can take specific measures to achieve their own goals.

The rest content of this paper can be summarized as follows. Section 2 presents the investigated model and corresponding assumptions. In Section 3, we study the steady state solutions and derive some main system performance measures. In Section 4, we get the individual equilibrium arrival rates by analyzing the properties of the customers' utility function. Section 5 gives the expressions of the social welfare and the cost function. Due to the complexity of their formulas, the Particle Swarm Optimization algorithm (PSO) is introduced to find the socially optimal arrival rates and the cost-optimal arrival rates. Section 6 shows the results of the numerical examples and Section 7 concludes this paper.

2 Model Description

In this section, we consider a constant retrial queue with balking and set-up time. Potential primary customers arrive in a Poisson process with rate

Λ

. Assuming that there is no waiting space in front of the server, an arriving customer who finds the server idle will take up it and receive service immediately, otherwise he could choose to enter the "virtual" retrial orbit waiting for retry or to balk, depending on his expected net payoff. Once a service is finished, only the head customer in the orbit can begin to request for service. The retrial time is exponentially distributed with rate

θ

. If a new customer arrives during the retrial time, he will interrupt the process and receive service at once. The service times for customers (both external and repeated) are independent and exponentially distributed with rate

μ

Every time the system becomes empty, the server will be turned down and won't be restarted until there is a customer arrives. Once activated, the server will go through a random opening time subjected to exponential distribution with parameter

α

. The customer who activated the server will automatically enter the retrial orbit and become the head of the retrial queue. It is assumed that the interarrival times, service times, retrial times and set-up times are mutually independent.

Assuming that every customer gains a profit of

R

units after completing the service, while has to pay for a waiting cost of

C

per unit time for remaining in the system. All customers are indistinguishable and rational to pursue the maximization of their own profits, and they have the rights to determine whether or not to join at their arrival instants, which forms a game among them. Explicitly, customers tend to enter when they gain more from the service than they pay for the cost, otherwise they prefer to balk. On the other hand, if the reward equals to the cost, it doesn't matter for customers whether to enter or to stop. To ensure that a customer who arrives during the idle period will always choose to enter, we assume that

R > \frac{C}{μ} .

(2.1)

In this paper, the almost unobservable case is investigated. We use the pair

{(I (t), N (t)), t \geq 0}

to describe the system at time

t

, where

I (t)

indicates the state of the server and

N (t)

shows the number of customers in the orbit. Explicitly,

I (t) = {\begin{cases} 0, & if the server is idle, \\ 1, & if the server is busy, \\ 2, & if the server is in set-up time. \end{cases}

(2.2)

Then

{(I (t), N (t)), t \geq 0}

is a two-dimensional continuous time Markov chain, and its state space is

{(i, j), i = 0, 1, 2; j \geq 0}

. According to the above analysis, the joining probabilities of arriving customers depend on

I (t)

. Define

λ_{i} = Λ q_{i}, i = 0, 1, 2

, where

q_{i}

is the joining probability that specifies a general strategy, and

λ_{i}

becomes the effective arrival rate at state

i

, which reflects the customer's real demand rate for the service.

Because of the assumption (2.1), we have that

λ_{0} = Λ

. In the following analysis, we only need to study how do customers make decision at state

I (t) = 1, 2

, and we focus on the corresponding effective arrival rates

λ_{1}

and

λ_{2}

. According to Economou & Kanta^[13], the steady-state condition of this model is given by

ρ = \frac{λ_{1} (Λ + θ)}{μ θ} < 1.

(2.3)

The transition rate diagram of this model is shown in Figure 1.

Figure 1 Transition rate diagram of a retrial queue with balking and set-up time

Full size|PPT slide

3 Steady State Solutions

For the convenience to analyze the equilibrium strategies, we first study the steady state solutions. Suppose that the system is stable and let

p (i, j)

be the steady-state probability of state

(i, j)

, then we can easily get the balance equations:

\begin{array}{rcl} (λ_{2} + α) p (2, 1) = Λ p (0, 0), \end{array}

(3.1)

\begin{array}{rcl} (λ_{2} + α) p (2, n) = λ_{2} p (2, n - 1), n \geq 2, \end{array}

(3.2)

\begin{array}{rcl} Λ p (0, 0) = μ p (1, 0), \end{array}

(3.3)

\begin{array}{rcl} (Λ + θ) p (0, n) = μ p (1, n) + α p (2, n), n \geq 1, \end{array}

(3.4)

\begin{array}{rcl} (λ_{1} + μ) p (1, 0) = θ p (0, 1), \end{array}

(3.5)

\begin{array}{rcl} (λ_{1} + μ) p (1, n) = Λ p (0, n) + λ_{1} p (1, n - 1) + θ p (0, n + 1), n \geq 1. \end{array}

(3.6)

The generating function technique is used to solve the equations. Define the partial generating functions as:

P_{0} (z) = \sum_{n = 0}^{\infty} z^{n} p (0, n), P_{1} (z) = \sum_{n = 0}^{\infty} z^{n} p (1, n), P_{2} (z) = \sum_{n = 1}^{\infty} z^{n} p (2, n) .

(3.7)

Then we can get the following results.

Theorem 1 For the almost unobservable $M / M / 1$ retrial queue with balking and set-up time, the probabilities that the server is idle, busy or in set-up period are, respectively given by

P_{0} (1) = \frac{Λ λ_{2} μ + α μ θ - Λ λ_{1} α - λ_{1} α θ}{α μ θ - Λ λ_{1} α - λ_{1} α θ} p (0, 0),

(3.8)

\begin{array}{rcl} P_{1} (1) = \frac{Λ λ_{2} (Λ + θ)}{α μ θ - Λ λ_{1} α - λ_{1} α θ} p (0, 0), \end{array}

(3.9)

\begin{array}{rcl} P_{2} (1) = \frac{Λ}{α} p (0, 0), \end{array}

(3.10)

where

p (0, 0) = \frac{α μ θ - Λ λ_{1} α - λ_{1} α θ}{Λ μ θ - Λ^{2} λ_{1} - Λ λ_{1} θ + Λ λ_{2} μ + α μ θ - Λ λ_{1} α - λ_{1} α θ + Λ^{2} λ_{2} + Λ λ_{2} θ} .

(3.11)

Proof Multiplying Equations (3.1)

\sim

(3.2) by

z^{n}

and summing up over all

n

, we derive the following equation:

(λ_{2} + α) P_{2} (z) = λ_{2} z P_{2} (z) + Λ p (0, 0) .

(3.12)

Similarly, from Equations (3.3)

\sim

(3.6), we have that

\begin{array}{rcl} (Λ + θ) P_{0} (z) - θ p (0, 0) = μ P_{1} (z) + α P_{2} (z), \end{array}

(3.13)

\begin{array}{rcl} (Λ + μ) P_{1} (z) = Λ P_{0} (z) - Λ p (0, 0) + λ_{1} z P_{1} (z) + \frac{θ}{z} P_{0} (z) - \frac{θ}{z} p (0, 0) . \end{array}

(3.14)

By some algebraic manipulations, we use

p (0, 0)

to express

P_{i} (z), i = 0, 1, 2

as:

\begin{array}{rcl} P_{2} (z) = \frac{Λ p (0, 0)}{α + λ_{2} (1 - z)}, \end{array}

(3.15)

\begin{array}{rcl} P_{1} (z) = \frac{Λ + \frac{θ}{z}}{μ + λ_{1} (1 - z)} [P_{0} (z) - p (0, 0)], \end{array}

(3.16)

\begin{array}{rcl} P_{0} (z) = \frac{α}{Λ + θ - \frac{μ (Λ + θ / z)}{μ + λ_{1} (1 - z)}} P_{2} (z) + \frac{θ - \frac{μ (Λ + θ / z)}{μ + λ_{1} (1 - z)}}{Λ + θ - \frac{μ (Λ + θ / z)}{μ + λ_{1} (1 - z)}} p (0, 0) . \end{array}

(3.17)

Taking (3.15) into (3.17), then we have,

\begin{array}{rcl} P_{0} (z) \\ = & \frac{Λ α [μ + λ_{1} (1 - z)] - μ (Λ + θ / z) [α + λ_{2} (1 - z)] + θ [α + λ_{2} (1 - z)] [μ + λ_{1} (1 - z)]}{[α + λ_{2} (1 - z)] {(Λ + θ) [μ + λ_{1} (1 - z)] - μ (Λ + θ / z)}} p (0, 0) . \end{array}

(3.18)

Noticed that,

P_{0} (z)

and

P_{1} (z)

are both indeterminate forms when

z = 1

, so we use the L' Hospital rule to solve them and we have (3.8)

\sim

(3.10). Taking them into the normalization condition:

P_{0} (1) + P_{1} (1) + P_{2} (1) = 1

, we derive

p (0, 0)

as given by (3.11).

Based on the above proof process, we can immediately derive

P_{i}^{'} (z), i = 0, 1, 2

by differentiating (3.15), (3.16) and (3.18). Letting

z = 1

, we find that

\begin{array}{rcl} P_{0}^{'} (1) = \frac{μ}{Λ + θ} P_{1}^{'} (1) + \frac{Λ λ_{2}}{α (λ + θ)} \cdot p (0, 0), \end{array}

(3.19)

\begin{array}{rcl} P_{1}^{'} (1) = [\frac{- Λ λ_{2} θ}{(α μ θ - Λ λ_{1} α - λ_{1} α θ)} + \frac{(Λ + θ) (Λ λ_{2}^{2} μ θ + Λ λ_{2} α μ θ - Λ λ_{1} λ_{2}^{2} θ - Λ^{2} λ_{1} λ_{2}^{2})}{(α μ θ - Λ λ_{1} α - λ_{1} α θ)^{2}}] p (0, 0), \end{array}

(3.20)

\begin{array}{rcl} P_{2}^{'} (1) = \frac{Λ λ_{2}}{α^{2}} p (0, 0) . \end{array}

(3.21)

P_{i}^{'} (1), i = 0, 1, 2

can be considered as the contribution of state

i

to the expected number of customers in the orbit. As the three states are connected, customers accumulating in a single state will affect the other states.

Next we turn our attention to investigate the mean sojourn time(including service time) of a singled out customer. Assuming that an arriving customer decides to enter the system, and becomes the

j

th customer in the orbit. We denote the expected sojourn time of the specific customer at different states as

T_{i} (j), i = 0, 1, 2

. Then we obtain

T_{i} (j), i = 0, 1, 2

in the following analysis.

Lemma 1 For the almost unobservable $M / M / 1$ retrial queue with balking and set-up time, the mean sojourn times of the $j$ th customer in the orbit at steady state $I (t) = 0, 1, 2$ are, respectively given by

\begin{array}{rcl} T_{0} (j) = j (\frac{1}{θ} + \frac{Λ + θ}{μ θ}), \end{array}

(3.22)

\begin{array}{rcl} T_{1} (j) = j (\frac{1}{θ} + \frac{Λ + θ}{μ θ}) + \frac{1}{μ}, \end{array}

(3.23)

\begin{array}{rcl} T_{2} (j) = j (\frac{1}{θ} + \frac{Λ + θ}{μ θ}) + \frac{1}{α} . \end{array}

(3.24)

Proof Through state transition analysis, we have the following equations:

\begin{array}{rcl} T_{1} (0) = \frac{1}{μ}, \end{array}

(3.25)

\begin{array}{rcl} T_{0} (j) = \frac{1}{Λ + θ} + \frac{Λ}{Λ + θ} T_{1} (j) + \frac{θ}{Λ + θ} T_{1} (j - 1), \end{array}

(3.26)

\begin{array}{rcl} T_{1} (j) = \frac{1}{λ_{1} + μ} + \frac{λ_{1}}{λ_{1} + μ} T_{1} (j) + \frac{μ}{λ_{1} + μ} T_{0} (j), \end{array}

(3.27)

\begin{array}{rcl} T_{2} (j) = \frac{1}{λ_{2} + α} + \frac{λ_{2}}{λ_{2} + α} T_{2} (j) + \frac{α}{λ_{2} + α} T_{0} (j) . \end{array}

(3.28)

Combining equations (3.26) and (3.27), we have the recursive form of

T_{1} (j), j \geq 1

T_{1} (j) = T_{1} (j - 1) + \frac{1}{θ} + \frac{Λ + θ}{μ θ}, j \geq 1.

(3.29)

Considering to (3.25), we have that,

T_{1} (j) = T_{1} (0) + j (\frac{1}{θ} + \frac{Λ + θ}{μ θ}) = j (\frac{1}{θ} + \frac{Λ + θ}{μ θ}) + \frac{1}{μ}, j \geq 0.

(3.30)

Taking the expression of

T_{1} (j)

into (3.26), we derive

T_{0} (j)

as in (3.22). Furthermore, we have

T_{2} (j)

by substituting

T_{0} (j)

in (3.28).

For a non-specific new arriving customer, the situation is different, but we can also get the mean sojourn time with the help of Lemma1. Denote

W_{i}, (i = 0, 1, 2)

as the mean sojourn times of a new arriving customer who finds that

I (t) = 0, 1, 2

. We have the following conclusion.

Theorem 2 For the almost unobservable $M / M / 1$ retrial queue with balking and set-up time, the mean sojourn times of a new arriving customer who finds that the server is in idle, busy or set-up period are, respectively given by

\begin{array}{rcl} W_{0} = 1 / μ, \end{array}

(3.31)

\begin{array}{rcl} W_{1} = \frac{Λ + μ + θ}{μ θ} (\frac{λ_{2}}{α} + \frac{μ θ}{μ θ - Λ λ_{1} - λ_{1} θ}) + \frac{Λ + θ}{μ θ} + \frac{Λ}{θ (Λ + θ)}, \end{array}

(3.32)

\begin{array}{rcl} W_{2} = \frac{Λ + μ + θ}{μ θ} \cdot \frac{λ_{2}}{α} + \frac{Λ α + α μ + α θ + μ θ}{α μ θ} . \end{array}

(3.33)

Proof First of all, any customer arrives at idle state will enter the system and immediately be served, so the sojourn time equals to the mean service time

\frac{1}{μ}

What needs to be concerned is that in busy or set-up period cases. Assume that the server is busy and there are already

k

customers in the orbit, if a new customer decides to enter the system, he will be the

(k + 1)

th customer in the orbit, whose mean sojourn time is

T_{1} (k + 1)

. Using the PASTA property, we denote

P (k | 1) = \frac{p (1, k)}{\sum_{n = 0}^{\infty} p (1, k)} = \frac{p (1, k)}{P_{1} (1)}, k \geq 0

as the conditional probability that there are

k

customers in the orbit, given that the server is busy. According to the total probability formula, we derive that,

\begin{array}{rcl} W_{1} & = & \sum_{k = 0}^{\infty} T_{1} (k + 1) P (k | 1) \\ = & \frac{\sum_{k = 0}^{\infty} T_{1} (k + 1) p (1, k)}{P_{1} (1)} \\ = & \frac{\sum_{k = 0}^{\infty} [(k + 1) (\frac{1}{θ} + \frac{Λ + θ}{μ θ}) + \frac{1}{μ}] \cdot p (1, k)}{P_{1} (1)} \\ = & \frac{\sum_{k = 0}^{\infty} k (\frac{1}{θ} + \frac{Λ + θ}{μ θ}) p (1, k)}{P_{1} (1)} + \frac{\sum_{k = 0}^{\infty} (\frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{μ}) \cdot p (1, k)}{P_{1} (1)} \\ = & (\frac{1}{θ} + \frac{Λ + θ}{μ θ}) \cdot \frac{P_{1}^{'} (1)}{P_{1} (1)} + \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{μ}, \end{array}

where

\frac{P_{1}^{'} (1)}{P_{1} (1)}

can be computed by (3.9) and (3.20) as

\frac{P_{1}^{'} (1)}{P_{1} (1)} = - \frac{θ}{Λ + θ} + \frac{λ_{2} μ θ + α μ θ - λ_{1} λ_{2} θ - Λ λ_{1} λ_{2}}{α μ θ - Λ λ_{1} α - λ_{1} α θ} .

Combining the two equations and by some algebraic computation, we get the expression of

W_{1}

as in (3.32). Meanwhile, using the same argument, we obtain that,

\begin{array}{rcl} W_{2} = \sum_{k = 1}^{\infty} T_{2} (k + 1) P (k | 2) & = & (\frac{1}{θ} + \frac{Λ + θ}{μ θ}) \cdot \frac{P_{2}^{'} (1)}{P_{2} (1)} + \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α} \\ = & (\frac{1}{θ} + \frac{Λ + θ}{μ θ}) \cdot \frac{λ_{2}}{α} + \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α}, \end{array}

which can be converted to (3.33).

Theorem 2 reflects an important fact that

W_{2}

only depends on

λ_{2}

. Although

W_{1}

is related to the effective arrival rates both in busy and set-up time. As long as

λ_{2}

is determined,

W_{1}

is considered to be subject to

λ_{1}

only. This can be helpful for the following equilibrium analysis.

4 Individual Equilibrium

In this section, we aim to derive the individual equilibrium strategies in different states. Since the self-optimizing arriving customers are indistinguishable, and have the right to decide whether to join or not, it is reasonable to regard them as players in a symmetric game, whose strategies are balking or joining. For simplicity, a Nash equilibrium strategy is the one that the tagged customer has to adopt to maximize his benefit when all others take the same strategy. According to the game theory, there exists an equilibrium joining strategy. That is to say, the equilibrium arrival rates can be specified. According to the assumption of the reward-cost structure, we have the expression of the customers' benefit functions in state

I (t) = 1, 2

as:

\begin{array}{rcl} S_{1} (λ_{1}, λ_{2}) = R - C W_{1} \\ = R - C [\frac{Λ + μ + θ}{μ θ} (\frac{λ_{2}}{α} + \frac{μ θ}{μ θ - Λ λ_{1} - λ_{1} θ}) + \frac{Λ + θ}{μ θ} + \frac{Λ}{θ (Λ + θ)}], \end{array}

(4.1)

\begin{array}{rcl} S_{2} (λ_{2}) = R - C W_{2} = R - C [\frac{Λ + μ + θ}{μ θ} \cdot \frac{λ_{2}}{α} + \frac{Λ α + α μ + α θ + μ θ}{α μ θ}] . \end{array}

(4.2)

Then we have the following results.

Theorem 3 For the almost unobservable $M / M / 1$ retrial queue with balking and set-up time,

1)

when the server is in set-up period, the individual equilibrium arrival rate is given by

λ_{2}^{e} = {\begin{cases} 0, & i f \frac{R}{C} \leq \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α}, \\ λ_{2}^{'}, & i f \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α} < \frac{R}{C} \leq \frac{Λ + μ + θ}{μ θ} \cdot \frac{Λ}{α} + \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α}, \\ Λ, & i f \frac{R}{C} > \frac{Λ + μ + θ}{μ θ} \cdot \frac{Λ}{α} + \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α} . \end{cases}

(4.3)

2)

when the server is busy, there are three cases, and the individual equilibrium arrival rates are given as:

(a)

When $\frac{R}{C} \leq \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α}$ , i.e., $λ_{2}^{e} = 0$ ,

λ_{1}^{e} = {\begin{cases} 0, & i f \frac{R}{C} \leq \frac{Λ + μ + θ}{μ θ} + \frac{Λ + θ}{μ θ} + \frac{Λ}{θ (Λ + θ)}, \\ λ_{11}^{'}, & i f \frac{Λ + μ + θ}{μ θ} + \frac{Λ + θ}{μ θ} + \frac{Λ}{θ (Λ + θ)} < \frac{R}{C} \leq \frac{Λ + μ + θ}{μ θ - Λ^{2} - Λ θ} + \frac{Λ + θ}{μ θ} + \frac{Λ}{θ (Λ + θ)}, \\ Λ, & i f \frac{R}{C} > \frac{Λ + μ + θ}{μ θ - Λ^{2} - Λ θ} + \frac{Λ + θ}{μ θ} + \frac{Λ}{θ (Λ + θ)} . \end{cases}

(4.4)

(b)

When $\frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α} < \frac{R}{C} \leq \frac{Λ + μ + θ}{μ θ} \cdot \frac{Λ}{α} + \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α}$ , i.e., $λ_{2}^{e} = λ_{2}^{'}$ ,

λ_{1}^{e} = {\begin{cases} 0, & i f \frac{1}{α} \leq \frac{Λ + θ}{μ θ} + \frac{Λ}{θ (Λ + θ)}, \\ λ_{12}^{'}, & i f \frac{Λ + θ}{μ θ} + \frac{Λ}{θ (Λ + θ)} < \frac{1}{α} \leq \frac{Λ + μ + θ}{μ θ - Λ^{2} - Λ θ} + \frac{Λ}{θ (Λ + θ)} - \frac{1}{θ}, \\ Λ, & i f \frac{1}{α} > \frac{Λ + μ + θ}{μ θ - Λ^{2} - Λ θ} + \frac{Λ}{θ (Λ + θ)} - \frac{1}{θ} . \end{cases}

(4.5)

(c)

When $\frac{R}{C} > \frac{Λ + μ + θ}{μ θ} \cdot \frac{Λ}{α} + \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α}$ , i.e., $λ_{2}^{e} = Λ$ ,

λ_{1}^{e} = {\begin{cases} 0, & i f \frac{R}{C} \leq \frac{Λ^{2} + Λ μ + Λ θ}{α μ θ} + \frac{Λ + μ + θ}{μ θ} + \frac{Λ + θ}{μ θ} + \frac{Λ}{θ (Λ + θ)}, \\ λ_{13}^{'}, & i f \frac{Λ^{2} + Λ μ + Λ θ}{α μ θ} + \frac{Λ + μ + θ}{μ θ} + \frac{Λ + θ}{μ θ} + \frac{Λ}{θ (Λ + θ)} < \frac{R}{C}, \\ a n d \frac{R}{C} \leq \frac{Λ (Λ + μ + θ)}{α μ θ} + \frac{Λ + μ + θ}{μ θ - Λ^{2} - Λ θ} + \frac{Λ + θ}{μ θ} + \frac{Λ}{θ (Λ + θ)}, \\ Λ, & i f \frac{R}{C} > \frac{Λ (Λ + μ + θ)}{α μ θ} + \frac{Λ + μ + θ}{μ θ - Λ^{2} - Λ θ} + \frac{Λ + θ}{μ θ} + \frac{Λ}{θ (Λ + θ)} . \end{cases}

(4.6)

Specifically, $λ_{2}^{'}$ is the unique root of the equation $R - C W_{2} (λ_{2}) = 0$ , and is given by

λ_{2}^{'} = (\frac{R}{C} - \frac{1}{θ} - \frac{Λ + θ}{μ θ} - \frac{1}{α}) \cdot \frac{α μ θ}{Λ + μ + θ} .

(4.7)

$λ_{1 i}^{'}, i = 1, 2, 3$ , are respectively the roots of the three formulas : $S_{1} (λ_{1}, 0) = 0$ ; $S_{1} (λ_{1}, λ_{2}^{'}) = 0$ ; $S_{1} (λ_{1}, Λ) = 0$ , and are given by

\begin{array}{rcl} λ_{11}^{'} = \frac{μ θ}{Λ + θ} - \frac{Λ + μ + θ}{Λ + θ} (\frac{R}{C} - \frac{Λ + θ}{μ θ} - \frac{Λ}{θ (Λ + θ)})^{- 1}, \end{array}

(4.8)

\begin{array}{rcl} λ_{12}^{'} = \frac{Λ μ θ + μ θ^{2} - Λ α μ - Λ^{2} α - 2 Λ α θ - α θ^{2}}{(Λ + θ) (Λ + α + θ)}, \end{array}

(4.9)

\begin{array}{rcl} λ_{13}^{'} = \frac{μ θ}{Λ + θ} - \frac{Λ + μ + θ}{Λ + θ} [\frac{R}{C} - \frac{Λ (Λ + μ + θ)}{α μ θ} - \frac{Λ + θ}{μ θ} - \frac{Λ}{θ (1 + θ)}]^{- 1} . \end{array}

(4.10)

Proof Similar to the above discussion, customers have to measure the losses and gains to make the decision on whether to join or not.

1)

If a customer observes that the server is in set-up period upon arriving, then his joining strategy is dependent on his benefit function

S_{2} (λ_{2})

. It can be intuitively found from (4.2) that

S_{2} (λ_{2})

is decreasing with

λ_{2}

, which leads an ATC(avoid the crowd) behavior of the customer, thus there exists a unique equilibrium arrival rate

λ_{2}^{e}

(see Hassin and Haviv^[14]). To derive

λ_{2}^{e}

, we have the following discuss:

(ⅰ) When

S_{2} (0) \leq 0

, i.e.,

\frac{R}{C} \leq \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α}

, then

S_{2} (λ_{2}) \leq 0

in every

λ_{2} \in [0, Λ]

. In this case, customers' benefits are always negative, hence nobody wants to enter the system, so there forms a equilibrium

λ_{2}^{e} = 0

, which is the first branch of (4.3).

(ⅱ) When

S_{2} (0) > 0

and

S_{2} (Λ) \leq 0

, i.e.,

\frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α} < \frac{R}{C} \leq \frac{Λ + μ + θ}{μ θ} \cdot \frac{Λ}{α} + \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α}

, since

S_{2} (λ_{2})

strictly decreases with

λ_{2}

, there is a unique root of

S_{2} (λ_{2}) = 0

(0, Λ]

, denoted by

λ_{2}^{'}

, which is exactly the equilibrium point. Because if

λ_{2} > λ_{2}^{'}

, new arriving customers will all choose to balk since their benefits are negative, thus their strategies are equal to zero. This is against to the equilibrium property that all customers adopt the same strategy. On the other hand, the arrival rate which is less than

λ_{2}^{'}

will lead an "all joining" strategy and finally converge to

λ_{2}^{'}

, too. Therefore,

λ_{2}^{'}

is the unique equilibrium point of this branch.

(ⅲ) When

S_{2} (Λ) > 0

, i.e.,

\frac{R}{C} > \frac{Λ + μ + θ}{μ θ} \cdot \frac{Λ}{α} + \frac{1}{θ} + \frac{Λ + θ}{μ θ} + \frac{1}{α}

, the situation is completely opposite to (a), and all customers choose to enter since their benefits are always positive, which leads to a equilibrium of

λ_{2}^{e} = Λ

. This forms the last branch of (4.3).

2)

Theorem 2 tells that, once

λ_{2}

is determined,

W_{1}

is only dependent with

λ_{1}

, so as the customers' benefit function in busy state, which can be remarked as

S_{1} (λ_{1})

. Similarly, it can be found from (4.1) that

S_{1} (λ_{1})

is decreasing with

λ_{1}

when

λ_{2}

is settled. Thus, there exists three cases according to the value of

λ_{2}

in (4.3), which respectively correspond to (a), (b), (c) in Theorem 3. Proceeding the analysis as before, the proof of (4.4), (4.5) and (4.6) can be done, and

λ_{11}^{'}

λ_{12}^{'}

λ_{13}^{'}

are, respectively derived by solving the equations:

S_{1} (λ_{1}, 0) = 0

;

S_{1} (λ_{1}, λ_{2}^{'}) = 0

;

S_{1} (λ_{1}, Λ) = 0

There is one thing to notice in the above analysis: The process of deriving

λ_{1}^{e}

has preconditions in the three cases. In each case, we discuss three branches and present

λ_{1}^{e}

as in (4.4)

\sim

(4.6) for brevity and clarity. However, when there is a conflict between the precondition and the branch condition, that branch will be naturally canceled.

5 Social Optimization

In this section, we seek for social optimization for the social planner and the service provider, respectively, since they are out of different considerations. For the former, the goal is to maximize social welfare, while for the latter, reducing the total cost is the emphases.

5.1 Social Welfare

First, we investigate the social welfare, which is the sum of all the customers' expected net benefits. The expression of the social welfare is given by

\begin{array}{rcl} S (λ_{1}, λ_{2}) & = & Λ (R - \frac{C}{μ}) P_{0} (1) + λ_{1} (R - C W_{1}) P_{1} (1) + λ_{2} (R - C W_{2}) P_{2} (1) \\ = & Λ (R - \frac{C}{μ}) \cdot \frac{Λ λ_{2} μ + α μ θ - Λ λ_{1} α - λ_{1} α θ}{Λ μ θ - Λ^{2} λ_{1} - Λ λ_{1} θ + Λ λ_{2} μ + α μ θ - Λ λ_{1} α - λ_{1} α θ + Λ^{2} λ_{2} + Λ λ_{2} θ} \\ + λ_{1} [R - C (\frac{Λ + μ + θ}{μ θ} \cdot \frac{λ_{2}}{α} + \frac{Λ + μ + θ}{μ θ - Λ λ_{1} - λ_{1} θ} + \frac{(Λ + θ)^{2} + Λ μ}{μ θ (Λ + θ)})] \\ \times \frac{Λ λ_{2} (Λ + θ)}{Λ μ θ - Λ^{2} λ_{1} - Λ λ_{1} θ + Λ λ_{2} μ + α μ θ - Λ λ_{1} α - λ_{1} α θ + Λ^{2} λ_{2} + Λ λ_{2} θ} \\ + λ_{2} [R - C (\frac{Λ + μ + θ}{μ θ} \cdot \frac{λ_{2}}{α} + \frac{Λ α + α μ + α θ + μ θ}{α μ θ})] \\ \times \frac{Λ μ θ - Λ^{2} λ_{1} - Λ λ_{1} θ}{Λ μ θ - Λ^{2} λ_{1} - Λ λ_{1} θ + Λ λ_{2} μ + α μ θ - Λ λ_{1} α - λ_{1} α θ + Λ^{2} λ_{2} + Λ λ_{2} θ} . \end{array}

(5.1)

The purpose of the social planner is to maximize

S (λ_{1}, λ_{2})

by seeking the optimal arrival rates

λ_{1}^{*}

λ_{2}^{*}

, thus we can model the socially optimal problem as

max_{λ_{1}, λ_{2} \in [0, Λ]} S (λ_{1}, λ_{2})

. Unfortunately, the expression of

S (λ_{1}, λ_{2})

seems especially complex. Through trial and explore, we have to admit that it's too difficult to find the analytic solution. However, after consulting the literatures and analyzing our own model, we find it appropriate to adopt the Particle Swarm Optimization (PSO) algorithm to derive the numerical solutions.

At the mention of PSO algorithm, the most significant advantage is that it does not require too much analyticity of the objective function. It is an optimization algorithm based on swarm intelligence theory. In each iteration search process, Particles in swarm can dynamically adjust their position and speed by tracking two extremes of swarm: The best solution found by the particle itself, namely P-best, and the best solution found by the swarm, namely G-best. Through multiple iterations, the global optimal solution can be found. The specific process is presented in numerical examples.

5.2 Cost Analysis

In this subsection, we carry out the cost analysis from the service provider's point. The expenses come from many aspects, but can be simplified into the following four items:

C_{k}

= cost of the server per unit time for keeping a customer in the orbit;

C_{b}

= cost of the server per unit time for providing service;

C_{s}

= cost of the server per unit time during the set-up period;

C_{θ}

= cost of the server per unit time for retry.

Therefore we set up the expected total cost function per unit time as

C (λ_{1}, λ_{2}) = C_{k} [P_{0}^{'} (1) + P_{1}^{'} (1) + P_{2}^{'} (1)] + C_{b} μ + C_{s} α + C_{θ} θ,

(5.2)

where

P_{0}^{'} (1)

P_{1}^{'} (1)

and

P_{2}^{'} (1)

are given by (3.19)

\sim

(3.21). Aiming to minimize the total cost, service providers seek for the cost-optimal arrival rates. First we investigate the situation that customers are not allowed to balk. In this case, we denote that

λ_{1} = λ_{2} = λ

, and the cost function is written as:

\begin{array}{rcl} C (λ) \\ = & C_{b} μ + C_{s} α + C_{θ} θ + C_{k} \cdot \frac{α μ θ - λ^{2} α - λ α θ}{λ^{2} (μ - α) + λ θ (μ - α) + α μ θ} \\ \times [\frac{- λ^{2} θ (λ + μ + θ)}{(λ + θ) (α μ θ - λ^{2} α - λ α θ)} + \frac{λ^{2} (λ + μ + θ) (λ μ θ + μ θ - λ^{2} θ - λ^{3})}{(α μ θ - λ^{2} α - λ α θ)^{2}} + \frac{λ^{2} (λ + α + θ)}{α^{2} (λ + θ)}] . \end{array}

(5.3)

Due to the highly nonlinearity and complexity of the expression, we adopt the quadratic interpolation method to give the numerical solution. The basic idea of quadratic interpolation method is the continuous use of quadratic polynomials to approximate objective function

C (s)

in search intervals, and the minimum point of objective function is gradually approximated by the minimum point of interpolation polynomial. The main steps are as follows:

Step 0 Set the initial three points

s_{0} < s_{1} < s_{2}

, which satisfy

C (s_{1}) < C (s_{0})

, and

C (s_{2}) < C (s_{0})

. Choose the stopping tolerance as

ϵ = 10^{- 4}

Step 1 If

| s_{2} - s_{0} | \leq ϵ

, stop and output that

s^{*} \approx s_{1}

Step 2 According to the interpolation formula

\bar{s} = \frac{(s_{1} + s_{2}) C (s_{0}) - 2 (s_{0} + s_{2}) C (s_{1}) + (s_{0} + s_{1}) C (s_{2})}{2 (C (s_{0}) - 2 C (s_{1}) + C (s_{2}))}

, compute

\bar{s}

and

C (\bar{s})

. If

C (s_{1}) < C (\bar{s})

, turn to Step 4; otherwise go to Step 3.

Step 3 If

s_{1} > \bar{s}

, update

s_{2} = s_{1}

s_{1} = \bar{s}

C (s_{2}) = C (s_{1})

C (s_{1}) = C (\bar{s})

, and turn to Step 1; if not, update

s_{0} = s_{1}

s_{1} = \bar{s}

C (s_{0}) = C (s_{1})

C (s_{1}) = C (\bar{s})

, and then turn to Step 1.

Step 4 If

s_{1} < \bar{s}

, let

s_{2} = \bar{s}

C (s_{2}) = C (\bar{s})

and go to Step 1; otherwise let

s_{0} = \bar{s}

C (s_{0}) = C (\bar{s})

, and then turn to Step 1.

Here we assume that

C_{k} = 1

C_{b} = 2

C_{s} = 7

C_{θ} = 2

. Using the software Matlab, after several iterations, the cost-optimal arrival rate is shown in Table 1 with the error controlled by

ϵ = 10^{- 4}

. It is clearly that the solution converges to

λ_{c}^{*} = 1.0808

, and the minimal cost is

C (λ_{c}^{*}) = 44.8751

Table 1 The quadratic interpolation method in the constant retrial queue with set-up time

Iterations	$s_{0}$	$s_{1}$	$s_{2}$	$\bar{s}$	$f (\bar{s})$	Tolerance
0	0.2000	0.8000	1.4000	0.2000	44.9939	1.2000
1	0.7572	0.8000	0.8428	0.7572	44.9172	0.0855
2	0.0637	0.8000	1.5363	0.0637	44.9994	1.4725
3	0.5711	0.8000	1.0289	0.5711	44.9506	0.4579
4	0.3757	0.8000	1.2243	0.3757	44.8764	0.8486
5	1.0166	1.1204	1.2243	1.1204	44.8764	0.2077
6	1.0311	1.0758	1.0758	1.0758	44.8752	0.0447
7	1.0534	1.0758	1.0981	1.0981	44.8754	0.0447
8	1.0758	1.0804	1.0850	1.0804	44.8751	0.0092
9	1.0804	1.0808	1.0812	1.0804	44.8751	0.0008
10	1.0808	1.0808	1.0808	1.0808	44.8751	0.0000

Now, we turn our attention to the more general case, in which customers are allowed to balk, then the cost function is given by

\begin{array}{rcl} C (λ_{1}, λ_{2}) & = & C_{b} μ + C_{s} α + C_{θ} θ + C_{k} \cdot p (0, 0) \cdot [\frac{- Λ λ_{2} θ (Λ + μ + θ)}{(Λ + θ) (α μ θ - Λ λ_{1} α - λ_{1} α θ)} \\ + \frac{Λ λ_{2} (Λ + μ + θ) (λ_{2} μ θ + α μ θ - λ_{1} λ_{2} θ - Λ λ_{1} λ_{2})}{(α μ θ - Λ λ_{1} α - λ_{1} α θ)^{2}} + \frac{Λ λ_{2}}{α (Λ + θ)} + \frac{Λ λ_{2}}{α^{2}}] . \end{array}

(5.4)

Similar to the analysis of the social welfare, we can also use the PSO algorithm to solve the optimization problem. The difference is that the cost-optimal arrival rates we seek are to minimize the objective function. To do this, we just need to add a minus sign before the objective function

C (λ_{1}, λ_{2})

in the corresponding program. Section 6 gives the specific analysis process.

6 Numerical Examples

In this section, we use numerical experiments to intuitively reflect the impact of main parameters, i.e.,

R

α

μ

θ

, on the discussed arrival rates respectively. The expressions of the individual equilibrium arrival rate (

λ_{1}^{e}

λ_{2}^{e}

) are clearly given by Theorem 3. As for the socially optimal arrival rate (

λ_{1}^{*}

λ_{2}^{*}

) and the cost-optimal arrival rate (

λ_{1 c}^{*}

λ_{2 c}^{*}

), we have to adopt the PSO algorithm to analyze.

6.1 To the Individual Equilibrium Arrival Rate

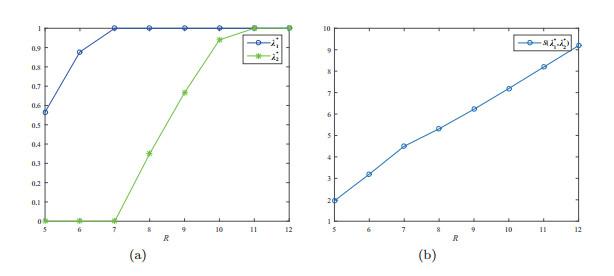
We choose one of the cases in Theorem 3 to explain the influence of the related parameters on

(λ_{1}^{e}, λ_{2}^{e})

. The graphical representations of the main results are shown in Figures 2

\sim

Figure 2 The individual equilibrium arrival rates $λ_{1}^{e}$ , $λ_{2}^{e}$ with respect to $α$ when $R = 8, C = 2, Λ = 2, μ = 3, θ = 3$

Full size|PPT slide

Figure 3 The individual equilibrium arrival rates $λ_{1}^{e}$ , $λ_{2}^{e}$ with respect to $μ$ when $R = 8, C = 2, Λ = 10, α = 1, θ = 5$

Full size|PPT slide

Figure 4 The individual equilibrium arrival rates $λ_{1}^{e}$ , $λ_{2}^{e}$ with respect to $θ$ when $R = 8, C = 2, Λ = 10, α = 1, μ = 5$

Full size|PPT slide

Firstly, it can be known from Figure 2 that there exists the opposite tendency of

λ_{1}^{e}

and

λ_{2}^{e}

with regard to

α

. It's reasonable that with the decreasing of the set-up time, customers finding the server at state 2 are more willing to enter the system. On the other hand, as long as the net benefit is positive, selfish customers will always choose to enter, which results in the congestion of the system. Therefore, the customer's arrival rate at busy state decreases correspondingly.

Secondly, it is easily understood that the service rate

μ

and the retrial rate

θ

have the same influence on

λ_{1}^{e}

and

λ_{2}^{e}

. Because the expected waiting time decreases as the decline of the mean service time or the retrial interval, customers spend less time and expenses in queue, surely the equilibrium arrival rates will increase. Figures 3

\sim

4 also support this point.

6.2 To the Socially Optimal Arrival Rate

In this section, we adopt the PSO algorithm to investigate the effect of parameters

R, α, μ, θ

on the socially optimal arrival rates

(λ_{1}^{*}, λ_{2}^{*})

and social welfare

S (λ_{1}^{*}, λ_{2}^{*})

, respectively.

Firstly, it is obvious that the socially optimal arrival rates and the social welfare are all increase with reward

R

when

R > 7

. When

R \leq 7

, the socially optimal arrival rate at state 2 is zero. The reason is that the net payoff of the latter arrivals would result in the loss of the earlier. From the social manager's point of view, since the reward is less than the loss, he would rather there is no customer entering the orbit during set-up time. However, when

R

is large enough, the total benefits brought by the customers are always higher than the cost, to maximize the social welfare, social manager would encourage people to join the system. Therefore,

λ_{1}^{*}

and

λ_{2}^{*}

achieve the maximization

Λ

gradually. Noticed that,

S (λ_{1}^{*}, λ_{2}^{*})

is almost increasing linearly with

R

due to its structure.

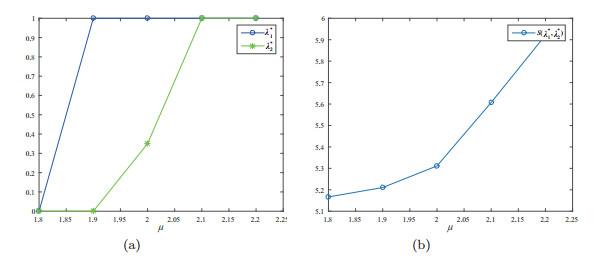
Secondly, Figure 6 shows that both

λ_{1}^{*}, λ_{2}^{*}

and

S (λ_{1}^{*}, λ_{2}^{*})

are increasing with parameter

α

in general, for the mean sojourn time decreases with set-up time, and the net benefits increases correspondingly. But compared with

λ_{2}^{*}

λ_{1}^{*}

reached its maximum earlier. The reason is that the server doesn't provide service during set-up time. When

α < 0.3

, the cost incurred by the customers entering at state 2 is more than the benefit they brought, so at this situation, social manager prefers there is no enter when the server is setting up. However, since

α \geq 0.3

λ_{2}^{*}

increases rapidly to its maximum. Because from then on, the set up time is sufficiently short, customers arriving at state 2 don't have to wait so long, and the net benefits exceed their waiting cost.

**Figure 5 The effect of $R$ on the socially optimal arrival rates $λ_{1}^{}$ , $λ_{2}^{}$ and social welfare $S (λ_{1}^{}, λ_{2}^{})$ for $Λ = 1, μ = 2, α = 3, θ = 3, C = 2$**

Full size|PPT slide

**Figure 6 The effect of $α$ on the socially optimal arrival rates $λ_{1}^{}$ , $λ_{2}^{}$ and social welfare $S (λ_{1}^{}, λ_{2}^{})$ for $Λ = 1, μ = 3, θ = 3, R = 8, C = 2$**

Full size|PPT slide

Finally, similar to the analysis in Section 6.1,

λ_{1}^{*}

and

λ_{2}^{*}

have the same trends with respect to

μ

and

θ

, and Figures 7

\sim

8 also show the evidence. So, we only study the impact of the service rate

μ

λ_{1}^{*}

λ_{2}^{*}

and

S (λ_{1}^{*}, λ_{2}^{*})

. From Figure 7(a) we can see that when

μ < 1.8

, both

λ_{1}^{*}

and

λ_{2}^{*}

are equal to 0. Intuitively, the smaller service rate results in the negative expected benefit of all the customers. When

1.8 \leq μ < 1.9

λ_{1}^{*}

begin to increase while

λ_{2}^{*}

is still equal to 0. Because the positive net payoff of customers arriving after the system activated can offset the negative effect of customers arriving at set-up period. As

μ > 1.9

, the service rate is large enough to avoid the congestion of the system, therefore

λ_{2}^{*}

also increases gradually to its maximum. Figure 7(b) shows that the social welfare is strictly increasing with respect to

μ

, since the larger the service rate, the shorter the mean service time. Therefore customers spend less time in queue and incur less cost.

**Figure 7 The effect of $μ$ on the socially optimal arrival rates $λ_{1}^{}$ , $λ_{2}^{}$ and social welfare $S (λ_{1}^{}, λ_{2}^{})$ for $Λ = 1, α = 3, θ = 3, R = 8, C = 2$**

Full size|PPT slide

**Figure 8 The effect of $θ$ on the socially optimal arrival rates $λ_{1}^{}$ , $λ_{2}^{}$ and social welfare $S (λ_{1}^{}, λ_{2}^{})$ for $Λ = 1, μ = 3, α = 3, R = 8, C = 2$**

Full size|PPT slide

6.3 To the Cost-Optimal Arrival Rate

Now we focus on the impact of parameters

α

μ

θ

from the perspective of the service provider. Through a large number of numerical experiments, we found that compared with other parameters, when

θ

takes a smaller value, the total cost

C (λ_{1}, λ_{2})

always reaches its minimum at

λ_{2} = 0

. That is because the retrial interval is too large for the server that will cause congestion of the system. Meanwhile, customers arriving at set-up time will only aggravate this problem since the server can't provide service during this period. Therefore, from the service provider's point, they would better prevent customers from entering at the set-up time. But when

θ

is large enough, it is shown that

λ_{1 c}^{*}

λ_{2 c}^{*}

and

C (λ_{1 c}^{*}, λ_{2 c}^{*})

have the following tendencies.

Figure 9(a) shows that when

α < 1

, due to the long set-up time, the set-up cost is too high for the service provider, so the system is better shuttled down. As

α

increases, the cost-optimal arrival rates and the total cost all increase accordingly. Because the set-up cost decreases, and the service provider needs the reward brought by customers to offset the cost. Thus customers are encouraged to enter the system and

λ_{1 c}^{*}

λ_{2 c}^{*}

increase. Figure 9(b) shows that as the number of customers increase, the cost for remaining customers in the orbit rises, and becomes the dominant player. Therefore, although the set-up cost decrease, the total cost continues to rise.

Figure 9 The effect of $α$ on the socially optimal arrival rates $λ_{1 c}^{}$ , $λ_{2 c}^{}$ and total cost $C (λ_{1 c}^{}, λ_{2 c}^{})$ for $Λ = 1, μ = 3, θ = 9, C_{b} = 2, C_{s} = 7, C_{θ} = 2, C_{k} = 1$

Full size|PPT slide

Figure 10 shows the tendency of

λ_{1 c}^{*}

λ_{2 c}^{*}

and

C (λ_{1 c}^{*}, λ_{2 c}^{*})

about parameter

θ

(

μ

has similar effect). As analyzed before, when

θ \leq 6

the cost-optimal arrival rates are

λ_{1} \in [0, Λ]

λ_{2} = 0

. As the increase of

θ

, the retrial interval gets shorter and the retrial cost decreases. Relatively the set-up cost is higher. Therefore, to avoid frequent set-up periods, the service provider should encourage potential customers to enter the system. Accordingly, the trends of

λ_{1 c}^{*}

λ_{2 c}^{*}

are upward curves. Meanwhile, more customers in the orbit means more keeping cost, so

C (λ_{1 c}^{*}, λ_{2 c}^{*})

increases correspondingly.

Figure 10 The effect of $θ$ on the socially optimal arrival rates $λ_{1 c}^{}$ , $λ_{2 c}^{}$ and total cost $C (λ_{1 c}^{}, λ_{2 c}^{})$ for $Λ = 1, μ = 3, α = 2, C_{b} = 2, C_{s} = 7, C_{θ} = 2, C_{k} = 1$

Full size|PPT slide

7 Conclusion

In this paper, we studied the M/M/1 constant retrial queue with balking and set-up time. When the server's state is observable while the queue length is unknown, the individual equilibrium strategies and social optimization problems are considered. Firstly, under the stability condition, we derived the customers' mean sojourn times for different states, and obtained the individual equilibrium arrival rates by analyzing the benefit function of arriving customers. After that, the expression of the social welfare is given. From the point of the social manager, the optimal arrival rates are presented by PSO algorithm. Furthermore, we carried out cost analysis from the point of the service provider, and derived the cost-optimal arrival rates in two cases that whether customers are allowed to balk or not, respectively. Finally, the numerical examples were given to show the sensitivity of main system performance measures.

To further study, this work can be generalized in different directions. One extension is to consider the general service times. In addition, the optimal pricing strategies that equate the customers' equilibrium arrival rates to the socially optimal arrival rates can be studied. Furthermore, the equilibrium analysis in other information levels could also be considered.

References

Publishing order | Descend order by publishing year | Descend order by cited within

1	Falin G, Templeton J. Retrial queues. Monographs on Statistics & Applied Probability, 1997. Cited in this article [1]

2	Artalejo J R. A queueing system with returning customers and waiting line. Operations Research Letters, 1995, 17, 191- 199. https://doi.org/10.1016/0167-6377(95)00017-E Cited in this article [1]

3	Artalejo J R, Gomez-Corral A. Steady state solution of a single-server queue with linear repeated requests. Journal of Applied Probability, 1997, 34, 223- 233. https://doi.org/10.2307/3215189 Cited in this article [1]

4	Artalejo J R, Gomez-Corral A. Analysis of a stochastic clearing system with repeated attempts. Stochastic Models, 1998, 14, 623- 645. https://doi.org/10.1080/15326349808807492 Cited in this article [1]

5	Fayolle G. A simple telephone exchange with delayed feedbacks. Proceedings of the International Seminar on Teletraffic Analysis and Computer Performance Evaluation, 1986, 245- 253. Cited in this article [1]

6	Falin G I. The M/M/1 retrial queue with retrials due to server failures. Queueing Systems, 2008, 58, 155- 160. https://doi.org/10.1007/s11134-008-9065-x Cited in this article [1]

7	Artalejo J R, Gomez-Corral A. Retrial Queueing Systems: A Computational Approach. Springer, Berlin, 2008. Cited in this article [1]

8	Naor P. The regulation of queue size by levying tolls. Econometrica, 1969, 37, 15- 24. https://doi.org/10.2307/1909200 Cited in this article [1]

9	Edelson Noel M, Hilderbrand D K. Congestion tolls for Poisson queuing processes. Econometrica, 1975, 43 (1): 81- 92. https://doi.org/10.2307/1913415 Cited in this article [1]

10	Burnetas A, Economou A. Equilibrium customer strategies in a single server Markovian queue with setup times. Queueing Systems, 2007, 56, 213- 228. https://doi.org/10.1007/s11134-007-9036-7 Cited in this article [1]

11	Zhang Y, Wang J. Equilibrium pricing in an M/G/1 retrial queue with reserved idle time and setup time. Applied Mathematical Modelling, 2017, 49, 514- 530. https://doi.org/10.1016/j.apm.2017.05.017 Cited in this article [1]

12	Yutaka S, Yoshitaka T, Yutaka T, et al. A composite queue with vacation/set-up/close-down times for svcc in IP over atm networks. Journal of the Operations Research Society of Japan, 1998, 41 (1): 68- 80. https://doi.org/10.15807/jorsj.41.68 Cited in this article [1]

13	Economou A, Kanta S. Equilibrium customer strategies and social-profit maximization in the single-server constant retrial queue. Naval Research Logistics, 2011, 58 (2): 107- 122. https://doi.org/10.1002/nav.20444 Cited in this article [1]

14	Hassin R, Haviv M. To Queue or not to queue: Equilibrium behavior in queueing systems. Springer US, 2003. Cited in this article [1]

Acknowledgements

The authors gratefully acknowledge the editor and two anonymous referees for their insightful comments and helpful suggestions that led to a marked improvement of the article.

Funding

the National Natural Science Foundation of China(61773014)

Postgraduate Research & Practice Innovation Program of Jiangsu Province China(SJKY19_0277)

PDF(441 KB)

184

Accesses

Citation

Detail

Sections

Recommended

Abstract
Key words
Cite this article
1 Introduction
2 Model Description
Figure 1 Transition rate diagram of a retrial queue with balking and set-up time
3 Steady State Solutions
4 Individual Equilibrium
5 Social Optimization
5.1 Social Welfare
5.2 Cost Analysis
Table 1 The quadratic interpolation method in the constant retrial queue with set-up time
6 Numerical Examples
6.1 To the Individual Equilibrium Arrival Rate
Figure 2 The individual equilibrium arrival rates $λ_{1}^{e}$ , $λ_{2}^{e}$ with respect to $α$ when $R = 8, C = 2, Λ = 2, μ = 3, θ = 3$
Figure 3 The individual equilibrium arrival rates $λ_{1}^{e}$ , $λ_{2}^{e}$ with respect to $μ$ when $R = 8, C = 2, Λ = 10, α = 1, θ = 5$
Figure 4 The individual equilibrium arrival rates $λ_{1}^{e}$ , $λ_{2}^{e}$ with respect to $θ$ when $R = 8, C = 2, Λ = 10, α = 1, μ = 5$
6.2 To the Socially Optimal Arrival Rate
Figure 5 The effect of $R$ on the socially optimal arrival rates $λ_{1}^{*}$ , $λ_{2}^{*}$ and social welfare $S (λ_{1}^{*}, λ_{2}^{*})$ for $Λ = 1, μ = 2, α = 3, θ = 3, C = 2$
Figure 6 The effect of $α$ on the socially optimal arrival rates $λ_{1}^{*}$ , $λ_{2}^{*}$ and social welfare $S (λ_{1}^{*}, λ_{2}^{*})$ for $Λ = 1, μ = 3, θ = 3, R = 8, C = 2$
Figure 7 The effect of $μ$ on the socially optimal arrival rates $λ_{1}^{*}$ , $λ_{2}^{*}$ and social welfare $S (λ_{1}^{*}, λ_{2}^{*})$ for $Λ = 1, α = 3, θ = 3, R = 8, C = 2$
Figure 8 The effect of $θ$ on the socially optimal arrival rates $λ_{1}^{*}$ , $λ_{2}^{*}$ and social welfare $S (λ_{1}^{*}, λ_{2}^{*})$ for $Λ = 1, μ = 3, α = 3, R = 8, C = 2$
6.3 To the Cost-Optimal Arrival Rate
Figure 9 The effect of $α$ on the socially optimal arrival rates $λ_{1 c}^{*}$ , $λ_{2 c}^{*}$ and total cost $C (λ_{1 c}^{*}, λ_{2 c}^{*})$ for $Λ = 1, μ = 3, θ = 9, C_{b} = 2, C_{s} = 7, C_{θ} = 2, C_{k} = 1$
Figure 10 The effect of $θ$ on the socially optimal arrival rates $λ_{1 c}^{*}$ , $λ_{2 c}^{*}$ and total cost $C (λ_{1 c}^{*}, λ_{2 c}^{*})$ for $Λ = 1, μ = 3, α = 2, C_{b} = 2, C_{s} = 7, C_{θ} = 2, C_{k} = 1$
7 Conclusion
References
Acknowledgements
Funding

Received	Accepted	Published
2019-06-19	2020-04-24	2020-06-25
Issue Date
2020-06-25

Please choose a citation manager

Content to export

Abstract

Key words

Cite this article

1 Introduction

2 Model Description

Figure 1 Transition rate diagram of a retrial queue with balking and set-up time

3 Steady State Solutions

4 Individual Equilibrium

5 Social Optimization

5.1 Social Welfare

5.2 Cost Analysis

Table 1 The quadratic interpolation method in the constant retrial queue with set-up time

6 Numerical Examples

6.1 To the Individual Equilibrium Arrival Rate

Figure 2 The individual equilibrium arrival rates $λ_{1}^{e}$ , $λ_{2}^{e}$ with respect to $α$ when $R = 8, C = 2, Λ = 2, μ = 3, θ = 3$

Figure 3 The individual equilibrium arrival rates $λ_{1}^{e}$ , $λ_{2}^{e}$ with respect to $μ$ when $R = 8, C = 2, Λ = 10, α = 1, θ = 5$

Figure 4 The individual equilibrium arrival rates $λ_{1}^{e}$ , $λ_{2}^{e}$ with respect to $θ$ when $R = 8, C = 2, Λ = 10, α = 1, μ = 5$

6.2 To the Socially Optimal Arrival Rate

**Figure 5 The effect of $R$ on the socially optimal arrival rates $λ_{1}^{}$ , $λ_{2}^{}$ and social welfare $S (λ_{1}^{}, λ_{2}^{})$ for $Λ = 1, μ = 2, α = 3, θ = 3, C = 2$**

**Figure 6 The effect of $α$ on the socially optimal arrival rates $λ_{1}^{}$ , $λ_{2}^{}$ and social welfare $S (λ_{1}^{}, λ_{2}^{})$ for $Λ = 1, μ = 3, θ = 3, R = 8, C = 2$**

**Figure 7 The effect of $μ$ on the socially optimal arrival rates $λ_{1}^{}$ , $λ_{2}^{}$ and social welfare $S (λ_{1}^{}, λ_{2}^{})$ for $Λ = 1, α = 3, θ = 3, R = 8, C = 2$**

**Figure 8 The effect of $θ$ on the socially optimal arrival rates $λ_{1}^{}$ , $λ_{2}^{}$ and social welfare $S (λ_{1}^{}, λ_{2}^{})$ for $Λ = 1, μ = 3, α = 3, R = 8, C = 2$**

6.3 To the Cost-Optimal Arrival Rate

Figure 9 The effect of $α$ on the socially optimal arrival rates $λ_{1 c}^{}$ , $λ_{2 c}^{}$ and total cost $C (λ_{1 c}^{}, λ_{2 c}^{})$ for $Λ = 1, μ = 3, θ = 9, C_{b} = 2, C_{s} = 7, C_{θ} = 2, C_{k} = 1$

Figure 10 The effect of $θ$ on the socially optimal arrival rates $λ_{1 c}^{}$ , $λ_{2 c}^{}$ and total cost $C (λ_{1 c}^{}, λ_{2 c}^{})$ for $Λ = 1, μ = 3, α = 2, C_{b} = 2, C_{s} = 7, C_{θ} = 2, C_{k} = 1$

7 Conclusion

{{custom_sec.title}}

{{custom_sec.title}}

References

{{custom_fnGroup.title_en}}

Footnotes

Acknowledgements

{{custom_ack.title_en}}

Funding

Share

模态框（Modal）标题

Please choose a citation manager

Content to export

Abstract

Key words

Cite this article

1 Introduction

2 Model Description

Figure 1 Transition rate diagram of a retrial queue with balking and set-up time

3 Steady State Solutions

4 Individual Equilibrium

5 Social Optimization

5.1 Social Welfare

5.2 Cost Analysis

Table 1 The quadratic interpolation method in the constant retrial queue with set-up time

6 Numerical Examples

6.1 To the Individual Equilibrium Arrival Rate

Figure 2 The individual equilibrium arrival rates λ1e, λ2e with respect to α when R=8,C=2,Λ=2,μ=3,θ=3

Figure 3 The individual equilibrium arrival rates λ1e, λ2e with respect to μ when R=8,C=2,Λ=10,α=1,θ=5

Figure 4 The individual equilibrium arrival rates λ1e, λ2e with respect to θ when R=8,C=2,Λ=10,α=1,μ=5

6.2 To the Socially Optimal Arrival Rate

Figure 5 The effect of R on the socially optimal arrival rates λ1∗, λ2∗ and social welfare S(λ1∗,λ2∗) for Λ=1,μ=2,α=3,θ=3,C=2

Figure 6 The effect of α on the socially optimal arrival rates λ1∗, λ2∗ and social welfare S(λ1∗,λ2∗) for Λ=1,μ=3,θ=3,R=8,C=2

Figure 7 The effect of μ on the socially optimal arrival rates λ1∗, λ2∗ and social welfare S(λ1∗,λ2∗) for Λ=1,α=3,θ=3,R=8,C=2

Figure 8 The effect of θ on the socially optimal arrival rates λ1∗, λ2∗ and social welfare S(λ1∗,λ2∗) for Λ=1,μ=3,α=3,R=8,C=2

6.3 To the Cost-Optimal Arrival Rate

Figure 9 The effect of α on the socially optimal arrival rates λ1c∗, λ2c∗ and total cost C(λ1c∗,λ2c∗) for Λ=1,μ=3,θ=9,Cb=2,Cs=7,Cθ=2,Ck=1

Figure 10 The effect of θ on the socially optimal arrival rates λ1c∗, λ2c∗ and total cost C(λ1c∗,λ2c∗) for Λ=1,μ=3,α=2,Cb=2,Cs=7,Cθ=2,Ck=1

7 Conclusion

{{custom_sec.title}}

{{custom_sec.title}}

References

{{custom_fnGroup.title_en}}

Footnotes

Acknowledgements

{{custom_ack.title_en}}

Funding

Figure 2 The individual equilibrium arrival rates $λ_{1}^{e}$ , $λ_{2}^{e}$ with respect to $α$ when $R = 8, C = 2, Λ = 2, μ = 3, θ = 3$

Figure 3 The individual equilibrium arrival rates $λ_{1}^{e}$ , $λ_{2}^{e}$ with respect to $μ$ when $R = 8, C = 2, Λ = 10, α = 1, θ = 5$

Figure 4 The individual equilibrium arrival rates $λ_{1}^{e}$ , $λ_{2}^{e}$ with respect to $θ$ when $R = 8, C = 2, Λ = 10, α = 1, μ = 5$

**Figure 5 The effect of $R$ on the socially optimal arrival rates $λ_{1}^{}$ , $λ_{2}^{}$ and social welfare $S (λ_{1}^{}, λ_{2}^{})$ for $Λ = 1, μ = 2, α = 3, θ = 3, C = 2$**

**Figure 6 The effect of $α$ on the socially optimal arrival rates $λ_{1}^{}$ , $λ_{2}^{}$ and social welfare $S (λ_{1}^{}, λ_{2}^{})$ for $Λ = 1, μ = 3, θ = 3, R = 8, C = 2$**

**Figure 7 The effect of $μ$ on the socially optimal arrival rates $λ_{1}^{}$ , $λ_{2}^{}$ and social welfare $S (λ_{1}^{}, λ_{2}^{})$ for $Λ = 1, α = 3, θ = 3, R = 8, C = 2$**

**Figure 8 The effect of $θ$ on the socially optimal arrival rates $λ_{1}^{}$ , $λ_{2}^{}$ and social welfare $S (λ_{1}^{}, λ_{2}^{})$ for $Λ = 1, μ = 3, α = 3, R = 8, C = 2$**

Figure 9 The effect of $α$ on the socially optimal arrival rates $λ_{1 c}^{}$ , $λ_{2 c}^{}$ and total cost $C (λ_{1 c}^{}, λ_{2 c}^{})$ for $Λ = 1, μ = 3, θ = 9, C_{b} = 2, C_{s} = 7, C_{θ} = 2, C_{k} = 1$

Figure 10 The effect of $θ$ on the socially optimal arrival rates $λ_{1 c}^{}$ , $λ_{2 c}^{}$ and total cost $C (λ_{1 c}^{}, λ_{2 c}^{})$ for $Λ = 1, μ = 3, α = 2, C_{b} = 2, C_{s} = 7, C_{θ} = 2, C_{k} = 1$