Crowdsourcing Task Assignment Mechanism Based on Employer Net Profit and Employee Satisfaction

Juan LI; Yu ZHANG

doi:10.21078/JSSI-2021-440-15

PDF(163 KB)

Journal of Systems Science and Information ›› 2021, Vol. 9 ›› Issue (4) : 440-454. DOI: 10.21078/JSSI-2021-440-15

Crowdsourcing Task Assignment Mechanism Based on Employer Net Profit and Employee Satisfaction

Author information +

History +

Abstract

Crowdsourcing task assignment has become an important task assignment model in the Internet economy era. In this paper, we study the crowdsourcing task assignment problem based on employer net profit and employee satisfaction. First, the reliability and interest of employees are modeled, based on which the mathematical expressions for employer net profit and employee satisfaction are given. Then, a multi-objective optimization problem is formulated to maximize employer net profit and employee satisfaction by jointly optimizing the task assignment matrix and task offer vector. Since the considered problem contains discrete variables, it cannot be solved directly by traditional optimization methods. Therefore, two low-complexity high-performance algorithms are proposed. The first algorithm is based on a fast non-dominated ranking genetic algorithm with an elite, which is able to explore the Pareto bound of the considered problem. The second algorithm is based on a reinforcement learning framework, which is able to maximize the weighted sum of employer net profit and employee satisfaction. Numerical results show that the number of tasks assigned to employees affects both employee satisfaction and employer net profit. The Pareto bounds and Pareto optimal solutions based on the solutions of the two proposed algorithms are also presented numerically, which quantitatively characterize the tradeoff between employer net profit and employee satisfaction.

Key words

crowdsourcing task assignment / satisfaction / reliability / interest

Cite this article

EndNote

Ris (Procite)

Bibtex

Download Citations

Juan LI , Yu ZHANG. Crowdsourcing Task Assignment Mechanism Based on Employer Net Profit and Employee Satisfaction. Journal of Systems Science and Information, 2021, 9(4): 440-454 https://doi.org/10.21078/JSSI-2021-440-15

1 Introduction

With the development of network technologies, more and more service industries perform task assignment based on crowdsourcing^[1]. In this mode, instead of assigning tasks to fixed employees, task publishers assign tasks according to certain rules based on the current situation. For the task publisher, this model can quickly find a large amount of available labor and expand the scope of services; for the employee, this model simplifies the process of finding a job and can gain some benefits. Compared with the traditional stable employment relationship, crowdsourcing task assignment shortens the employment cycle and increases the frequency of employment, and thus the game between task publishers and employees becomes more complicated. In the process of task assignment, crowdsourcing task assignment should consider both improving employee satisfaction to achieve employee retention and enhancing the vested profit of task publishers^[2].

First, in the context of the deep integration of the Internet and big finance, the competition among various task publishing platforms has gradually evolved into cultivating users' "loyalty" to the platform^[3]. In this process, retaining employees and ensuring the quality and durability of their services are more and more important to task publishers. Therefore, task publishers should focus on maintaining employee satisfaction. Furthermore, profit is the primary goal of task publishers in the task distribution process. However, there is a natural trade-off between task publisher's profit and employee satisfaction, which is further complicated by factors such as the quality of task completion^[4].

In the case of a takeaway platform, for example, the task publisher assigns orders to employees and receives a certain amount of profit from the merchant. In order to get more profit, both the task publisher and the employee want to get more orders. However, when an employee takes multiple order at the same time, the completion quality of each order may be affected, e.g., during the delivery process, the latter orders may cause users to negatively comment on the platform due to overtime, resulting in loss of profit. To ensure profits and service quality, task publishers should take into account the reliability of employees in completing tasks when assigning tasks. At the same time, employee satisfaction is influenced by subjective interest and objective access to rewards. Since the total profit of each task is fixed, there is a game between task publishers and employees in the distribution of profits^[5].

As tasks are continuously assigned, the reliability and satisfaction of employees are constantly changing; at the same time, task publisher have to balance vested interests and future interests for long-term development. Therefore, the current task assignment is not isolated, but is influenced by the results of past task assignments, which also affects the future task assignments. To this end, this paper studies the crowdsourcing task assignment problem based on task publishers' net profit and employee satisfaction. To describe the situation of employees undertaking tasks, the reliability and interest of employees are modeled, and quantitative mathematical expressions for task publisher net profit and employee satisfaction are given based on ^[6]. A multi-objective optimization problem^[7] is constructed to maximize task publisher net profit and employee satisfaction by jointly optimizing the task assignment matrix and task offer vector. Since the considered problem contains discrete variables, it cannot be solved directly by traditional optimization methods. For this reason, two low-complexity algorithms are proposed in this paper. The first algorithm is a search method constructed based on a fast non-dominated ranking genetic algorithm with an elite strategy^[8] to inscribe the Pareto optimality bound of the considered problem^[9]. The second algorithm is a weighted single objective function optimization algorithm constructed based on a reinforcement learning framework^[10]. Numerical results show that the number of tasks undertaken by each employee affects both employee satisfaction and employer net profit, and that employers should set the maximum number of tasks to be undertaken according to the employee profile. The numerical results also give Pareto optimal bounds and Pareto optimal solutions based on the solutions of the two proposed algorithms, which quantitatively characterize the tradeoff between employer net profit and employee satisfaction.

2 Model Description

Consider a typical crowdsourcing task assignment model, where a task publisher (later referred to as an "employer") is expected to complete

N

different types of tasks. For this purpose, the employer, through the task publishing platform, assigns

N

tasks to

K

employees. Both tasks and employees are considered as heterogeneous, i.e., the characteristics of the

N

tasks are different, and the competencies possessed by

K

employee are also different. Each employee can be assigned to more than one task, but not more than

B

at most, and each task is assigned to only one employee. This is common in take-out and delivery platforms when assigning tasks, for example, a rider can often deliver multiple orders at once, but each order will not be delivered by multiple riders. When assigning tasks, the employer gives a quotation for each task, and the

n

th task quotation is recorded as

b_{n}

. The quoted price will not exceed the profit available for completing the task, i.e.,

b_{n}^{(max)}

. Depending on the completion of the task, the employee will be paid accordingly, up to an upper limit of

b_{n}

. At the same time, the employer may also receive a commission, i.e., net profit, for this task, up to a maximum of

(b_{n}^{(max)} - b_{n})

In order to characterize the situation of employees undertaking tasks, each employee possesses two basic attributes, namely reliability and interest, defined as follows.

1) Employee Reliability. Facing the

n

th task, the reliability of the

k t h

employee's reliability is denoted as

R_{k, n}

to indicate the employee's completion of the task, and the range of values is

[0, 1]

where

R_{k, n} = 0

means incomplete and

R_{k n} = 1

indicates perfect completion. Since the task completion degree directly affects the task profit, the actual payoff for the

k

th employee to complete the

n

th task is

R_{k, n} b_{n}

and the net profit to the employer is

R_{k, n} (b_{n}^{(max)} - b_{n})

The characterization of employee reliability is an important issue in crowdsourcing task assignment. In this paper, the current reliability of employees is characterized based on the historical reliability and the current number of tasks, which is expressed as

R_{k, n} = min {r_{k, n} / (\exp (α_{k} * c_{k})), 1},

where

r_{k, n}

is a random number generated by normal distribution with a mean value of

[0, 1]

and variance of 1, and satisfying both

r_{k, n} = max {r_{k, n}, 0}

and

r_{k, n} = min {r_{k, n}, 1}

α_{k}

denotes the coefficient of the number of tasks for the

k

th employee. When

α_{k}

is larger, it indicates that the reliability of the employee is more affected by the number of tasks.

c_{k}

denotes the number of tasks currently assigned to the

k

th employee. It is worth noting that the mean value of

r_{k, n}

will be updated with the completion degree and number of completions of the task by the employee. When the task completion degree is high, the average value of

r_{k, n}

increases to 1; conversely, the average value of

r_{k, n}

decreases to 0. For each employee, the reward for completing tasks is related to both the number of tasks and the reliability. Therefore, the employer should take both into account when assigning tasks, avoiding both low pay due to a low number of tasks assigned to the employee and a decrease in the employee's reliability rating due to a high number of tasks assigned to the employee.

2) Employee interest. Faced with the

n

th task, the

k

th interest of the employee is expressed as

I_{k, n}

, which is used to indicate the subjective willingness of the employee to take up the task, and the value range is

[0, 1]

, where

I_{k, n} = 0

indicates that the employee does not want to undertake the task, and

I_{k, n} = 1

indicates a perfect desire to undertake the task. The interest is mainly influenced by the historical interest level and the current quotations, which is expressed as

I_{k, n} = min {i_{k, n} * \log (1 + 0.5 * b_{n}), 1},

where

i_{k, n}

is a random number generated by normal distribution with a mean value of

[0.5, 1]

and a variance of

1

, and satisfies both

i_{k, n} = max {i_{k, n}, 0}

and

i_{k, n} = min {i_{k, n}, 1}

. It is also worth noting that the mean and variance of

i_{k, n}

will be updated with the number of times the employee completes the task, and the employee's interest in a certain task will decrease as the number of times increases. Employers need to motivate employees by increasing the quotation.

When assigning tasks, the main indicators that employers need to consider are net profit and employee satisfaction, both of which are related to the reliability and interest of employee, as defined below.

1) Employer net profit. As mentioned above, the employer earns a net profit from the difference between the profit after the completion and the quoted price of the task. Assign

N

tasks, the total net profit obtained is

Γ = \sum_{n = 1}^{N} \sum_{k = 1}^{K} θ_{k, n} R_{k, n} (b_{n}^{(max)} - b_{n}),

where

θ_{k, n}

is the task assignment factor and takes the value

{0, 1}

. When

θ_{k, n} = 1

, it means that the

n

th task is assigned to the

k

th employee; when

θ_{k, n} = 0

, it means that the

n

th task is not assigned to the

k

th employee. Therefore, the number of tasks

c_{k}

assigned to

k

th employee can be expressed as

c_{k} = \sum_{n = 1}^{N} θ_{k, n} .

2) Employee satisfaction. Employee satisfaction is mainly determined by their interest in completing tasks and the payoff they receive, expressed as

Φ = \sum_{n = 1}^{N} \sum_{k = 1}^{K} θ_{k, n} (w_{1} I_{k, n} + w_{2} R_{k, n} b_{n}),

where

W_{1}

denotes the interest degree weighting coefficient, and

W_{2}

denotes the payoff weight coefficient and satisfies

w_{1} + w_{2} = 1

For employers, current net profit represents short-term benefits, while employee satisfaction represents long-term benefits, both of which are important. If the employer only focuses on completing the short-term benefits currently obtained, the employee will be poached by other task publishing platforms due to dissatisfaction with the job. This is common in Internet platforms such as takeaway, taxi, delivery, etc. Therefore, employers need to consider the current net profit and employee satisfaction when assigning tasks. In addition, there are some trade-offs in the task assignment process, for example, employees tend to get more tasks and thus more pay, but when an employee is assigned too many tasks, its completion of each task will be influenced, so employers need to balance the trade-off between employees' demands and task completion. The more employees are assigned the same type of task, the better they are at completing the task, but the lower their interest in the task. Therefore, employers need to balance the trade-off between employee interest and task completion. These relationships increase the complexity of problem analysis and solution, but also provide a broad scope for exploration.

3 Question Construction

In this paper, we consider the interests of employers and employees, and design a crowdsourcing task assignment mechanism to jointly maximize employers' profits and employees' satisfaction as the goal to achieve the best match between employees and tasks.

Let

\bm Ω = [θ_{k, n}]

denote the task assignment matrix, and

b = [b_{1}, b_{2}, \dots, b_{N}]

denote the offer vector, the multi-objective optimization problem under consideration can be modeled as

\begin{aligned} max_{Ω, b} Γ (Ω, b) \end{aligned}

(1a)

\begin{aligned} max_{Ω, b} Φ (Ω, b) \end{aligned}

(1b)

\begin{aligned} s . t . & (C 1) : \sum_{k = 1}^{K} θ_{k, n} = 1, \end{aligned}

(1c)

\begin{aligned} (C 2) : c_{k, n} \leq B, \end{aligned}

(1d)

\begin{aligned} (C 3) : 0 \leq b_{n} \leq b_{n}^{(m a x)}, \end{aligned}

(1e)

\begin{aligned} (C 4) : θ_{k, n} \in {0, 1}, \end{aligned}

(1f)

where constraint (C1) indicates that each task has and is only assigned to one user; constraint (C2) indicates that the total number of tasks shared by each user does not exceed

B

. constraint (C3) means that the offer of each task must not be higher than the task profit.

At the end of a batch, the employee's reliability and interest in the task will change, so when the next batch arrives, the employer will reassign the task based on the updated employee reliability and interest.

4 Solving Method

The problem under consideration is a multi-objective optimization problem and there is a trade-off between two objectives that are constrained to each other, i.e., the increase in the employer's total net profit/employer's satisfaction is at the cost of employee satisfaction/employer's total net profit. In addition, the problem under consideration has discrete variables (i.e., task assignment matrix) that are difficult to solve directly using traditional gradient solving methods (e.g., convex optimization theory). Given that task assignment problems are often large in scale and the task assignment process is demanding for time delay, this paper proposes two low-complexity solution methods based on genetic algorithms and reinforcement learning algorithms, respectively.

Both genetic algorithms and reinforcement learning algorithms can handle large-scale task assignment problems, and they are both non-gradient algorithms that can handle discrete variables or discontinuous functions. In contrast, the genetic algorithm can handle the considered problem and find the Pareto optimal solution without configuring hyperparameters, but when the reliability and interest of employees change, it needs to be calculated again; reinforcement learning requires multiple hyperparameters and multiple training episodes, and for the trained model, even if the reliability and interest of employees change, it can be directly derived from the constructed deep neural network. In general, genetic algorithms are better for single processing; reinforcement learning algorithms are better for long-term processing.

4.1 Genetic Algorithm-Based Task Assignment Method

The genetic algorithm simulates the biological evolution process by maintaining potential solutions from generation to generation and gradually approximating the optimal solution of the problem through population computation and stochastic search. The algorithm does not require prior background knowledge of the problem or additional hyperparameter settings, and is well adapted to problems of complex form and large size. Among many genetic algorithms, the fast and elitist non-dominated sorting generic algorithm (NSGA-II) with elitist strategy is considered as an effective method to solve multi-objective optimization problems, which can locate the Pareto optimal solution set of the problem under consideration.

For the problem under consideration, the feasible domain is defined as

χ = {Ω, b ∣ (C 1), (C 2), (C 3), (C 4)} .

For a feasible solution

x \in χ

, if there is no

y \in χ

, such that

Γ (y) \geq Γ (x)

and

Φ (y) \geq Φ (x)

hold simultaneously, then we claim

x

is a Pareto-optimal solution to the problem under consideration, and that

x

dominate

y

NSGA-II performs fast non-inferiority ranking based on the dominance relationship between feasible solutions to improve search efficiency and algorithm robustness. The core steps are summarized as follows.

1) Encoding and decoding. For the problem under consideration, the task assignment matrix

Ω

of each element takes the value of binary, i.e., 0 or 1, so no additional encoding is required. However, since the quote vector

b

is a continuous variable, each element of

b

is first discretized and then binary encoded. The value of the quotation

b_{n}

of the

n

th task is

{0, b_{n} / T, 2 b_{n} / T, \dots, (T + 1) b_{n} / T, b_{n}^{(max)}}

and the value of each quote is binary encoding, denoted as

\tilde{b_{n}}

. The binary quote vector composed of

\tilde{b_{n}}

is denoted as

\tilde{b}

. Combine all the quotes that satisfy the constraints

(C 1)

(C 2)

(C 3)

and

(C 4)

of the task assignment matrix and the encoded quotes form a genetic population set denoted as

\tilde{χ} = {Ω, \tilde{b}}

. When calculating the objective function value, it is necessary to

\tilde{b_{n}}

is recovered after decoding as

b_{n}

2) Generation of the initial population. Based on the set of constructed gene populations,

N I

feasible solutions are randomly selected from

\tilde{χ}

and recorded as individuals to form the initial population. Subsequently, the population is continuously updated by the selection mechanism, and the number of individuals in the population remains to be

N I

3) Fast non-dominated sorting. To speed up the search, the population is stratified according to the level of individual non-inferiority solutions. For the

i

th individual in the population, calculate the number

n_{i}

of individuals that dominate individual

i

and the set

S_{i}

of individuals dominated by individual

i

. On this basis, a fast non-inferiority stratification is performed, and the specific steps are: a) Find the individuals in the population

n_{i} = 0

of the population, i.e., the individuals that are not dominated by any other individuals, and save them to the current set

F_{1}

; b) For each individual in the set

F_{1}

, iterate through each individuals in the set

S_{i}

of the individuals it dominates, execute

n_{l} = n_{l} - 1

and saves

n_{l} = 0

to the set of individuals

H

, i.e., find the individuals other than individual

i

which is not dominated by any other individual except individual

l

; c) The individual obtained in the set

F_{1}

is the first non-dominated individual in the stratum with

H

. The above steps are repeated until the whole population is stratified.

4) Virtual fitness. Keeping the diversity of individuals in the population can avoid too much stacking of feasible solutions in local optimum. For this reason, virtual fitness is proposed in NSGA-II. The specific steps are: a) Initialize the distance between individuals in the same layer, so that

L [i]_{d} = 0

; b) To the individuals in the same stratum by the first

m (m \in {0, 1})

objective function values in ascending order; c) Make the individuals on the edge of the ranking have the selection advantage, and

L [0]_{d} = L [1]_{d} = M

; d) For the individuals in the sort, find the crowding distance

L [i]_{d} = L [i]_{d} + (L [i + 1]_{m} - L [i - 1]_{m})

; e) Repeat the above steps for different function values.

5) Selection operator. The selection operator improves the survival probability of high-performance individuals and reduces the loss of effective genes, which in turn optimizes the direction toward the Pareto optimal solution and makes the solution more homogeneous. Based on the non-dominated ordering and crowding distance calculation, each individual in the population

i

has two properties, i.e., non-dominated ordering and crowding distance. A round-robin selection operator is used to randomly select two individuals, and when two individuals have different non-dominated rankings, the individual with the lower ranking (i.e., less dominated) is selected; when two individuals have the same non-dominated ranking, the individual with the less crowded surrounding is selected.

6) Crossover and variation. The algorithm's local and global search performance is improved by changing the value of the last set of feasible solutions through crossover variation. For example, using simulated binary crossover (SBC), given a random crossover point, the parts of two parent individuals located on either side of the crossover point are exchanged.

7) Elite strategy. To prevent the loss of excellent solutions during random evolution, an elite retention mechanism is added. That is, an additional archive set is constructed to save the elite individuals searched during the evolution of the population, while the individuals in the archive set do not evolve directly. Due to the limitation of computational and storage resources, the archive set needs to be updated according to the Pareto relationship between the saved individuals and the individuals in the evolved population.

The process of solving the considered problem based on NSGA-II is summarized in the following algorithm.

Algorithm 1 NSGA-II-based task assignment method

Input: maximum number of genetic iterations, deviation of fitness function, population size, i.e., number of feasible solutions generated each time, optimal front-end individual coefficient ParetoFraction ∈ (0, 1).
Output: Task allocation strategy
1: Set NI=100, randomly generate a set of feasible solution sets
2: for iterations less than the maximum number of genetic iterations do　　
3:      Evolutionary population (crossover and variation), by changing the values of the previous set of feasible solutions through crossover variation to obtain a new set of feasible solutions 　　
4:      Perform fast non-dominated sorting 　　
5:      Calculating virtual fitness 　　
6:      Implement elite strategies to retain NI a viable solution 　　
7:      Based on this set of feasible solutions, calculate the current results of the two objective functions

Γ

Φ

　　
8: End For
9: End While

4.2 Reinforcement Learning Based Task Assignment Method

The multi-objective optimization problem can be transformed into a weighted single-objective optimization problem. Restricted by the choice of weight coefficients, compared with direct multi-objective optimization, weighted single-objective optimization will have some loss in optimality. However, solving the weighted single-objective optimization problem by reinforcement learning algorithm can greatly improve the efficiency of task assignment, adapt to the changing environment, and make rapid adjustments to task assignment.

The problem of optimizing task assignment based on crowdsourcing can be modeled as a Markov decision process (MDP) based problem, and such problems are suitable for solving using the

Q

-learning algorithm. The core of

Q

-learning is to build a

Q

-table containing all state-action pairs, and the learning process of

Q

-learning can be considered as a function approximation of state-action pairs, i.e., a function approximation of

Q

values. Each value in the table indicates how good or bad an action is taken by the agent in the current state, and the agent updates the values in the

Q

table through continuous interaction with the environment. When it is known that the intelligent body is in a certain state, the action that has the maximized

Q

value is selected as the action to be executed in the current state, and the

Q

value is updated by the following formula

Q (s, a) \leftarrow Q (s, a) + α [r + γ max Q (s^{'}, a^{'}) - Q (s, a)],

where

α

denotes the learning rate of the algorithm;

r

denotes the immediate reward of the environment after the agent performs action a in state;

γ

denotes the discount factor; and

s^{'}

denotes the next state after the agent performs the action

a

. Thus, this Q-learning algorithm can be defined as a quadratic Markov process

⟨ S, A, R, P ⟩

, where

S

denotes the state space;

A

denotes the action space;

R

denotes the reward function; and

P

denotes the probability of state transfer (which can be ignored when the model is determined).

In reinforcement learning, traditional

Q

-leaning algorithms have some limitations. For example,

Q

-learning uses a

Q

-table to store states and actions, and when there are many states-actions, the

Q

-table becomes very complex and too dimensional, which consumes a lot of time and memory space to find and store. In addition, in a crowdsourcing-based task assignment environment, a large number of tasks and multiple users are usually generated. In this case, a large number of actions are generated, and traditional

Q

-learning algorithms are clearly not applicable. For this reason, Deep

Q

Network (DQN) combines

Q

-learning with neural network to improve the

Q

-learning algorithm, which can effectively solve such defects of traditional

Q

-learning algorithm that cannot handle high-dimensional data, when the

Q

-value update formula is as follows.

Q (s, a ∣ θ) \leftarrow Q (s, a ∣ θ) + α [r + γ max Q (s^{'}, a^{'} ∣ θ) - Q (s, a ∣ θ)] .

In crowdsourcing tasks with a high number of states and actions, it is more appropriate to use DQN for solving them. In the model of DQN, the platform observes the environment state to assign appropriate tasks; the execution effect of these tasks (employee satisfaction, employer net profit, etc.) is fed back to the platform as reward values, and the platform again learns to assign tasks based on these choices and reward values to complete the training process of the model. The core of the work lies in 1) designing the corresponding action space and state space for the research content; 2) modeling the research content into a Markov decision process and 3) designing a suitable reward function.

1) Action space The action of the task assignment platform consists of a task assignment matrix

Ω

and a representation offer vector

b

. Since the action space of the value-based DQN algorithm must be finite, in the proposed DQN-based algorithm, the task assignment matrix

\bm Ω

and the discretized offer vector

b

as the set of feasible actions. Where, for the offer vector

b

, which is in the range of 0 to

b_{n}^{(max)}

is divided into

N

equal parts, we define the set

P = {0, \frac{b_{n}^{(max)}}{N - 1}, \frac{2 b_{n}^{(max)}}{N - 1}, \dots, b_{n}^{(max)}}

indicates an optional offer.

2) State space For the design of the state space, the following three points are considered: 1) Whether each task has and is assigned to only one user (constraint C1); 2) Whether the total number of tasks allocated to each user does not exceed

B

(constraint C2); and 3) the action selection in the current state. Based on this, note that

S

is the set of states, and for the

n

th employee, at the

t

-th iteration, define its

s \in S

state to be

s_{t}^{n} = {I_{t}^{i}, M_{t}^{i}, a_{t}^{i}},

where

I_{t}^{i}

denotes whether it is satisfied at the

t

-th iteration that each task has and is assigned to only one employee, defined as follows:

I_{t}^{n} = {\begin{array}{lr} 0, \sum_{k = 1}^{K} θ_{k, n} \neq 1; \\ 1, \sum_{k = 1}^{K} θ_{k, n} = 1. \end{array}

Similarly,

M_{t}^{i}

indicates whether the total number of tasks allocated to each employee does not exceed

B

, which is defined as

M_{t}^{n} = {\begin{array}{lr} 0, \sum_{k = 1}^{K} θ_{k, n} - B > 0; \\ 1, \sum_{k = 1}^{K} θ_{k, n} - B \leq 0. \end{array}

Also,

a_{t}^{n} \in A

indicates the action selection in the current state.

3) Reward function The reward function is the goal of the platform for task assignment. The degree of good or bad strategy of learning is essentially determined by the reward function, and only by designing the correct reward function can the platform achieve the purpose of learning through continuous iteration. In the task assignment process, each employee's task assignment has an impact on other users, and the satisfaction and profit generation of all employees jointly influence the effect of task assignment. Therefore, the reward function needs to jointly consider the objective of the optimization problem as well as the constraints.

For the optimization objective, the higher the employer's net profit, the higher the value of the reward function, and vice versa. Similarly, the higher the employee satisfaction, the higher the value of the reward function, and vice versa. For ease of processing, a weighted single objective function is used to represent the multi-objective function. The weighted sum of employer net profit and employee satisfaction can be directly considered as the reward function, which is given by

L_{t}^{n, k} = λ_{1} Γ_{t}^{n, k} + λ_{2} ϕ_{t}^{n, k},

where

λ_{1} \in (0, 1)

and

λ_{2} = 1 - λ_{1}

denotes the balance coefficient between total employee profit and employee satisfaction.

For the constraint, when each task is assigned to one user and only one user, the agent will receive a positive reward and vice versa with a larger penalty. Similarly, when the total number of tasks allocated to each user does not exceed

B

, the agent will also receive a positive reward, and vice versa. Thus, the constraint is expressed as

U_{t}^{n, k} = {\begin{cases} k_{a} + k_{b}, & \sum_{k = 1}^{K} θ_{k, n} = 1, \sum_{k = 1}^{K} θ_{k, n} - B \leq 0, \\ - k_{c} + k_{b}, & \sum_{k = 1}^{K} θ_{k, n} \neq 1, \sum_{k = 1}^{K} θ_{k, n} - B \leq 0, \\ k_{a} - k_{d}, & \sum_{k = 1}^{K} θ_{k, n} = 1, \sum_{k = 1}^{K} θ_{k, n} - B > 0, \\ - k_{c} - k_{d}, & \sum_{k = 1}^{K} θ_{k, n} \neq 1, \sum_{k = 1}^{K} θ_{k, n} - B > 0, \end{cases}

where

k_{a}, k_{b}, k_{c}, k_{d} \in (1, \infty)

denotes the reward or punishment received by the agent under whether the constraint is satisfied or not. When the constraints (C1) and (C2) are not satisfied, the reward will drop sharply. Conversely, when the constraint is satisfied, the agent receives a positive reward. That is, maximization

U_{t}^{n, k}

implies that constraints (C1) and (C2) can be satisfied. Therefore, the reward function is defined as

r_{t}^{n, k} = ω_{a} L_{t}^{n, k} + ω_{b} U_{t}^{n, k},

where

ω_{a}

and

ω_{b}

are the weight values to balance the rewards of the optimization objective and its constraints. Through the above construction of action space, state space, and reward function in this section, a DQN-based task assignment method is proposed, and the pseudo-code of this algorithm is as follows.

Algorithm 2 DQN-based task assignment algorithm

1: Initialize various parameters
2: while each round of iterations do
3: for each intelligent body do
4: Initialization state

s_{t}^{n, k}, t = 0

5:         while each time slot $t$ do
6:             Generate a random number between 0 and 1 rand(0, 1)
7:             if rand(0, 1)

< ε

then
8:                 Randomly select an action in the action set
9:             else
10:                 Select the action with the maximum Q value in the current state
11:                 EndIf
12:                #160; Execute the action

a_{t}^{n, k}

, get an immediate return

t_{t}^{n, k}

, and get the next state

s_{t + 1}^{n, k}

13: Deposit the experience gained

{s_{t}^{n, k}, a_{t}^{n, k}, r_{t}^{n, k}, s_{t + 1}^{n, k}}

into the experience pool
14:                  Random sampling of small batches from the experience pool
15:                 Update the Q value according to the X equation
16:                 Switching states, i.e.,

s_{t}^{n, k} = s_{t + 1}^{n, k}

17:                 if Current Iteration Number Maximum number of iterations then
18:                     Execute Step 3
19:                 else
20:                     Jump out judgment
21:                  Endif
22:                  EndFor
23:                  EndWhile

5 Simulation Results

Consider a typical crowdsourcing task assignment model. The number of tasks posted by the employer is set to 10, the profit of each task is set to 10, and the offer is divided into 10 level, i.e., the

{10 %, 20 %, \dots, 100 %}

of profit. The number of employees is set to 5, and the reliability and interest of employees for each task are randomly generated. Both the interest degree weighting factor and the payoff weighting factor are set to 0.5. The maximum number of tasks that each employee can undertake is set to 5. For the above values, there are a total of 9454621 task assignment matrices satisfying the constraints and a total of

10^{10}

offer vectors. Therefore, there are more than 9.4

\times

10^{16}

task assignment option. If we use the exhaustive method to traverse all task assignment options, we need to consume huge computational resources, and it is difficult to guarantee the timeliness of task assignment. The proposed two algorithms can significantly improve the task assignment efficiency and have the ability to adapt to the changes of user reliability and interest.

1) Maximum number of employee assignments versus employer net profit

Figure 1 plots the relationship between the number of tasks assigned to employees and employee profit. It can be seen that the optimal number of tasks to be assigned varies at different task quantity coefficients and the trend of variation is also different. For example, when the task quantity coefficient is 0.7, it means that the employee's reliability is influenced by the task quantity, so the employee profit decreases monotonically with the number of tasks undertaken. For example, when the number of tasks coefficient is 0.2, 0.3 and 0.4, the employee profit increases and then decreases with the number of tasks undertaken, and there is an optimal number of tasks undertaken. This result is consistent with real-life situations, such as when employees take on too many tasks, there is often a decline in the completion of individual tasks. Therefore, employers should set the maximum number of tasks to be undertaken according to employee characteristics when assigning tasks in order to obtain the maximum profit.

Figure 1 Relationship between the number of tasks assigned to employees and employee profit

Full size|PPT slide

2) Maximum number of tasks undertaken by employees and employee satisfaction

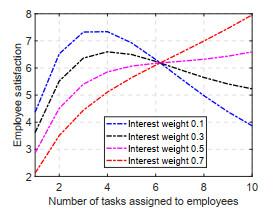
Figures 2 and 3 plot the relationship between the number of tasks assigned to employees and employee satisfaction with offer accounts being 40% and 80% of the profit, respectively. Employee satisfaction is generally higher when the offer accounts for a higher percentage, while employee satisfaction is more likely to be influenced by the amount of tasks undertaken by employees. This is because when the offer is high, employee compensation is the dominant factor in employee satisfaction, and when the amount of tasks undertaken by employees increases, the reliability of completing each task decreases, resulting in a decrease in the actual compensation received, and thus satisfaction is more likely to be influenced by the amount of tasks undertaken. On the contrary, when the offer is low, the interest of the employees increases in the satisfaction and is less influenced by the reward received. In addition, the weight of employees' interest in the task is also an important factor in the change of satisfaction and the number of tasks undertaken. The higher the interest weight of employees, the more stable the trend of satisfaction with the number of tasks undertaken. This shows that for employers, a single reliance on raising the task offer can improve employee satisfaction, but it is not conducive to stabilizing employee satisfaction, and cultivating employee interest in the task assignment process.

Figure 2 The relationship between the number of tasks assigned to employees and employee satisfaction (quoted as 80% of profit)

Full size|PPT slide

Figure 3 Relationship between the number of tasks assigned to employees and employee satisfaction (quoted 40% of profit)

Full size|PPT slide

3) Employee Satisfaction and Employer Net Profit Pareto Boundary

Figure 4 gives the Pareto boundaries for employee satisfaction and employer net profit. The compromise relationship between employee satisfaction and employer net profit is affected by profit distribution, and the effect of the number of tasks undertaken by employees on employee satisfaction and employer net profit makes the compromise relationship more complex. According to the proposed genetic algorithm the satisfaction-net profit domain can be carved out, and a larger satisfaction-net profit domain can be obtained compared to the random assignment algorithm. When using the reinforcement learning algorithm, the multi-optimization objective is changed to the weighted values of employer net profit and employee satisfaction, and thus the obtained results are related to the choice of weighting coefficients. With different weighting factors, the reinforcement learning algorithm can obtain different results on the Pareto boundary.

Figure 4 Pareto boundary

Full size|PPT slide

Figure 5 plots the results obtained by the reinforcement learning algorithm for different weighting factors. As mentioned earlier, the crowdsourcing task assignment problem includes task assignment matrix and task offer, which generate feasible solutions of great order of magnitude. While genetic algorithms can search for different Pareto solutions by discrete populations, reinforcement learning algorithms provide low-complexity solution algorithms. It is worth stating that the reinforcement learning algorithm performs dynamic online task assignment because of the variation in employee reliability and interest considered by the reinforcement learning algorithm.

Figure 5 Weighted sum of employer net profit and employee satisfaction

Full size|PPT slide

6 Summary

In this paper, we study the crowdsourcing task assignment problem and construct a multi-objective optimization problem to maximize employer net profit and employee satisfaction by jointly optimizing the task assignment matrix and the task offer vector. Since the problem under consideration contains discrete variables, it cannot be solved using convex optimization theory. For this reason, two low-complexity, high-performance algorithms are proposed in this paper. The first algorithm is a search method based on NSGA-II construction, which inscribes the Pareto optimality bound of the considered problem. The second one is a weighted single objective function solution algorithm based on reinforcement learning. Numerical results show that the number of tasks undertaken by each employee affects both employee satisfaction and employer net profit, and that employers should set the maximum number of tasks undertaken according to the employee profile. The numerical results also give Pareto optimal bounds and Pareto optimal solutions based on the two proposed algorithms, which quantitatively characterize the tradeoff between employer net profit and employee satisfaction.

To further improve the efficiency of task assignment, an algorithmic framework for generating labeled data with the help of genetic algorithms and then computing them through supervised learning will be investigated in the future.

References

Publishing order | Descend order by publishing year | Descend order by cited within

1	Lynch R, Young J C, Boakye-Achampong S, et al. Benefits of crowdsourcing for libraries: A case study from Africa. IFLA Journal, 2021, 47 (2): 168- 181. https://doi.org/10.1177/0340035220944940 Cited in this article [1]

2	Tian Y, Wang S, Ding E Y. Design, implementation and practice of big data and business intelligence system for retail industry. Systems Engineering-Theory & Practice, 2017, 37 (5): 1282- 1293. https://en.cnki.com.cn/Article_en/CJFDTotal-XTLL201705020.htm Cited in this article [1]

3	Jeon Y Y, et al. How does service environment enhance consumer loyalty in the sport fitness industry? The role of servicescape, cosumption motivation, emotional and flow experiences. Sustainability, 2021, 13 (11): 6414- 6414. https://doi.org/10.3390/su13116414 Cited in this article [1]

Tian H, Jiang C. An empirical study of the influence mechanism of social responsible human resource management on employees' innovative behavior: Based on the chain mediating effect of the perspective of labor relations. Journal of Guangdong University of Finance and Economics, 2020, 35 (6): 42- 50.

Cited in this article [1]

5	Yao P, Yao Z. Game analysis on the establishment of employee's compensation from the perspective of time difference. Soft Science, 2018, 32 (10): 58- 61. 58-61, 79 Cited in this article [1]

6	Shi Z, Xin Y, Sun Y, et al. Task allocation mechanism for crowdsourcing system based on reliability of users. Journal of Computer Applications, 2017, 37 (9): 2449- 2453. Cited in this article [1]

7	Pan W, Wang S, Hua G, et al. Multi-objective order allocation model under fuzzy weight. Chinese Journal of Management Science, 2009, 17 (2): 80- 85. Cited in this article [1]

8	Feng S, Ai Q. Application of fast and elitist non-dominated sorting generic algorithm in multi-objective reactive power optimization. Transactions of China Electrotechnical Society, 2007, (12): 146- 151. Cited in this article [1]

9	Zhang B, Xu L, Huang Z, et al. Multi-objective GANs pareto optimality algorithm using gradient strategy. Computer Engineering and Applications, 2021, 57 (9): 89- 95. Cited in this article [1]

10	Qin Z H, Li N, Liu X T, et al. Overview of research on model-free reinforcement learning. Computer Science, 2021, 48 (3): 180- 187. Cited in this article [1]

Acknowledgements

The authors gratefully acknowledge the editor and two anonymous referees for their insightful comments and helpful suggestions that led to a marked improvement of the article.

PDF(163 KB)

252

Accesses

Citation

Detail

Sections

Recommended

Received	Accepted	Published
2021-05-09	2021-07-31	2021-08-25
Issue Date
2021-08-25

Please choose a citation manager

Content to export

Abstract

Key words

Cite this article

1 Introduction

2 Model Description

3 Question Construction

4 Solving Method

4.1 Genetic Algorithm-Based Task Assignment Method

4.2 Reinforcement Learning Based Task Assignment Method

5 Simulation Results

Figure 1 Relationship between the number of tasks assigned to employees and employee profit

Figure 2 The relationship between the number of tasks assigned to employees and employee satisfaction (quoted as 80% of profit)

Figure 3 Relationship between the number of tasks assigned to employees and employee satisfaction (quoted 40% of profit)

Figure 4 Pareto boundary

Figure 5 Weighted sum of employer net profit and employee satisfaction

6 Summary

{{custom_sec.title}}

{{custom_sec.title}}

References

{{custom_fnGroup.title_en}}

Footnotes

Acknowledgements

{{custom_ack.title_en}}

Share

模态框（Modal）标题

Please choose a citation manager

Content to export

Abstract

Key words

Cite this article

1 Introduction

2 Model Description

3 Question Construction

4 Solving Method

4.1 Genetic Algorithm-Based Task Assignment Method

4.2 Reinforcement Learning Based Task Assignment Method

5 Simulation Results

Figure 1 Relationship between the number of tasks assigned to employees and employee profit

Figure 2 The relationship between the number of tasks assigned to employees and employee satisfaction (quoted as 80% of profit)

Figure 3 Relationship between the number of tasks assigned to employees and employee satisfaction (quoted 40% of profit)

Figure 4 Pareto boundary

Figure 5 Weighted sum of employer net profit and employee satisfaction

6 Summary

{{custom_sec.title}}

{{custom_sec.title}}

References

{{custom_fnGroup.title_en}}

Footnotes

Acknowledgements

{{custom_ack.title_en}}